Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
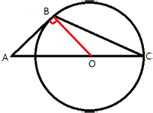OC является радиусом окружности R, AO=AC-OC.
Проведем отрезок BO. BO - так же является радиусом окружности. AB -
касательная к окружности, следовательно AB перпендикулярен BO (по
свойству касательной).
Значит треугольник ABO -
прямоугольный, тогда по
теореме Пифагора:
AO2=AB2+BO2
(AC-OC)2=AB2+R2
(25-R)2=152+R2
625-50R+R2=225+R2
625-225=50R
400=50R
R=8
D=2R=2*8=16
Ответ: D=16
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
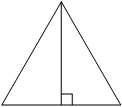Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
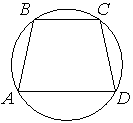Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
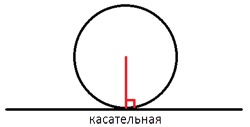
Комментарии: