
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ507 –Η–Ζ 1087 |
 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC. –Δ–Ψ―΅–Κ–Α O ―è–≤–Μ―è–Β―²―¹―è ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η―è –Ψ―² ―²–Ψ―΅–Κ–Η O –¥–Ψ ―²–Ψ―΅–Κ–Η A –Η –Ω―Ä―è–Φ―΄―Ö AD –Η AC ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ ―Ä–Α–≤–Ϋ―΄ 10, 9 –Η 6. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC. –Δ–Ψ―΅–Κ–Α O ―è–≤–Μ―è–Β―²―¹―è ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η―è –Ψ―² ―²–Ψ―΅–Κ–Η O –¥–Ψ ―²–Ψ―΅–Κ–Η A –Η –Ω―Ä―è–Φ―΄―Ö AD –Η AC ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ ―Ä–Α–≤–Ϋ―΄ 10, 9 –Η 6. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD.
 –ü–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι:
–ü–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι:
OF - ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, ―².–Κ. OF –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Η –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ
–Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι AC.
AG=AF
BG=BH=x
CH=CF=y
AF –Ϋ–Α–Ι–¥–Β–Φ –Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
AO2=AF2+OF2
102=AF2+62
100=AF2+36
AF2=64
AF=8=AG
EH -
–≤―΄―¹–Ψ―²–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. EH=OH+OE=6+9=15
SABC=p*r, –≥–¥–Β p - –Ω–Ψ–Μ―É–Ω–Β―Ä–Η–Φ–Β―²―Ä, r - ―Ä–Α–¥–Η―É―¹ –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η.
p=(AB+BC+AC)/2.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABC –Η CDA.
AD=BC –Η AB=CD (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α).
AC - –Ψ–±―â–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, –Ω–Ψ
―²―Ä–Β―²―¨–Β–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Α ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤, –¥–Α–Ϋ–Ϋ―΄–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ―Ä–Α–≤–Ϋ―΄.
–Δ–Ψ–≥–¥–Α:
SABCD=2*SABC
–‰ –≤ ―²–Ψ–Ε–Β –≤―Ä–Β–Φ―è SABCD=EH*AD.
–ü―Ä–Η―Ä–Α–≤–Ϋ―è–Β–Φ –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ―΄–Β ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Α:
p*r=EH*AD/2
(AB+BC+AC)/2*r=EH*BC/2
(AG+GB+BH+HC+CF+AF)*r=EH*(BH+HC)
(8+x+x+y+y+8)*6=15*(x+y)
(16+2x+2y)*6=15*(x+y)
96+6(2x+2y)=15*(x+y)
96+12(x+y)=15*(x+y)
96=3(x+y)
x+y=32=BC=AD
SABCD=EH*AD=15*32=480
–û―²–≤–Β―²: SABCD=480
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
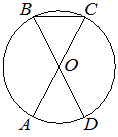 –£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ―²―Ä–Β–Ζ–Κ–Η AC –Η BD βÄî –¥–Η–Α–Φ–Β―²―Ä―΄. –Θ–≥–Ψ–Μ AOD ―Ä–Α–≤–Β–Ϋ 50¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ACB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ―²―Ä–Β–Ζ–Κ–Η AC –Η BD βÄî –¥–Η–Α–Φ–Β―²―Ä―΄. –Θ–≥–Ψ–Μ AOD ―Ä–Α–≤–Β–Ϋ 50¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ACB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
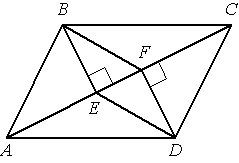 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β –ê–£–ΓD –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä―΄ –£–ï –Η DF –Κ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η –ê–Γ (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η BEF –Η DFE ―Ä–Α–≤–Ϋ―΄.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β –ê–£–ΓD –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä―΄ –£–ï –Η DF –Κ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η –ê–Γ (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η BEF –Η DFE ―Ä–Α–≤–Ϋ―΄.
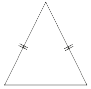 –ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 25, –Α –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β ―Ä–Α–≤–Ϋ–Ψ 30. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 25, –Α –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β ―Ä–Α–≤–Ϋ–Ψ 30. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
 –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Φ AB=BC –Η ∠ABC=25¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Φ AB=BC –Η ∠ABC=25¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 3, –Α –Ψ–¥–Η–Ϋ –Η–Ζ –Ω―Ä–Η–Μ–Β–≥–Α―é―â–Η―Ö –Κ –Ϋ–Β–Ι ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ 30¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Β―¹–Μ–Η –Β―ë –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 2 –Η 6.
–ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 3, –Α –Ψ–¥–Η–Ϋ –Η–Ζ –Ω―Ä–Η–Μ–Β–≥–Α―é―â–Η―Ö –Κ –Ϋ–Β–Ι ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Β–Ϋ 30¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –Β―¹–Μ–Η –Β―ë –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 2 –Η 6.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2014-05-29 09:40:10) –¥–Α―Ä―¨―è: ―¹–Ω–Α―¹–Η–±–Ψ –≤–Α–Φ, –≤―΄ –Φ–Ψ–Μ–Ψ–¥―Ü―΄!
(2014-05-28 20:38:47) –¥–Α―Ä―¨―è: ―¹–Ω–Α―¹–Η–±–Ψ –≤–Α–Φ, –≤―΄ –Φ–Ψ–Μ–Ψ–¥―Ü―΄!
(2014-05-27 15:11:09) –¥–Α―Ä―¨―è: ―¹–Ω–Α―¹–Η–±–Ψ –≤–Α–Φ, –≤―΄ –Φ–Ψ–Μ–Ψ–¥―Ü―΄!
(2014-05-26 15:10:37) –¥–Α―Ä―¨―è: ―¹–Ω–Α―¹–Η–±–Ψ –≤–Α–Φ, –≤―΄ –Φ–Ψ–Μ–Ψ–¥―Ü―΄!
(2014-05-21 17:06:20) –¥–Α―Ä―¨―è: ―¹–Ω–Α―¹–Η–±–Ψ –≤–Α–Φ, –≤―΄ –Φ–Ψ–Μ–Ψ–¥―Ü―΄!
(2014-05-21 10:14:06) –¥–Α―Ä―¨―è: ―¹–Ω–Α―¹–Η–±–Ψ –≤–Α–Φ, –≤―΄ –Φ–Ψ–Μ–Ψ–¥―Ü―΄!
(2014-05-20 22:09:43) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –î–Α―Ä―¨―è, ―¹–Ω–Α―¹–Η–±–Ψ –Η –£–Α–Φ!
(2014-05-20 21:39:24) –¥–Α―Ä―¨―è: ―¹–Ω–Α―¹–Η–±–Ψ –≤–Α–Φ, –≤―΄ –Φ–Ψ–Μ–Ψ–¥―Ü―΄!