
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ456 –Є–Ј 1087 |
 –Ю–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–і–Є—Г—Б–Њ–≤ 45 –Є 90 –Ї–∞—Б–∞—О—В—Б—П –≤–љ–µ—И–љ–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ. –Ґ–Њ—З–Ї–Є A –Є B –ї–µ–ґ–∞—В –љ–∞ –њ–µ—А–≤–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —В–Њ—З–Ї–Є C –Є D вАФ –љ–∞ –≤—В–Њ—А–Њ–є. –Я—А–Є —Н—В–Њ–Љ AC –Є BD вАФ –Њ–±—Й–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –њ—А—П–Љ—Л–Љ–Є AB –Є CD.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–і–Є—Г—Б–Њ–≤ 45 –Є 90 –Ї–∞—Б–∞—О—В—Б—П –≤–љ–µ—И–љ–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ. –Ґ–Њ—З–Ї–Є A –Є B –ї–µ–ґ–∞—В –љ–∞ –њ–µ—А–≤–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —В–Њ—З–Ї–Є C –Є D вАФ –љ–∞ –≤—В–Њ—А–Њ–є. –Я—А–Є —Н—В–Њ–Љ AC –Є BD вАФ –Њ–±—Й–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –њ—А—П–Љ—Л–Љ–Є AB –Є CD.
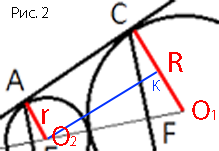
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ
—В—А–∞–њ–µ—Ж–Є—О ACO1O2
–Ф–∞–љ–љ–∞—П —В—А–∞–њ–µ—Ж–Є—П
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–∞—П, —В.–Ї. —А–∞–і–Є—Г—Б—Л –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л
–Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є AC (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є).
–Я—А–Њ–≤–µ–і–µ–Љ O2K –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ AC, O2K=AC, —В.–Ї. ACKO2 -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
 –Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
(O1O2)2=(O2K)2+(KO1)2
(R+r)2=(O2K)2+(R-r)2
(90+45)2=(O2K)2+(90-45)2
18225=(O2K)2+2025
(O2K)2=16200
O2K=10√
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є OAO2 –Є OCO1 (c–Љ. –†–Є—Б.1).
∠AOO2 - –Њ–±—Й–Є–є
∠OAO2=∠OCO1=90¬∞
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Н—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л (–њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤).
–Ґ–Њ–≥–і–∞, R/r=OC/OA
90/45=OC/OA=(OA+AC)/OA
2*OA=OA+10√
OA=10√
–Ш–Ј
–њ–Њ–і–Њ–±–Є—П —Н—В–Є—Е –ґ–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤:
R/r=O10/O2O
R/r=(O2O+R+r)/O2O
90/45=(O2O+90+45)/O2O
2(O2O)=O2O+135
O2O=135
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ —Г–≥–Њ–ї ∠AOO2 –Ї–∞–Ї α
cosα=OA/OO2=10√
–Я–Њ—Б–Љ–Њ—В—А–Є–Љ –љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є OAE –Є OCF.
–Ю–љ–Є
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ –њ–Њ
–≤—В–Њ—А–Њ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г —Е–Њ—А–і—Л.
–Ґ–Њ–≥–і–∞ –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ OAE:
cosα=OE/OA
OE=OA*cosα=10√
–Ф–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ OCF:
cosα=OF/OC
OF=OC*cosα=(OA+AC)*cosα=(10√
EF=OF-OE=240-120=120
–Ю—В–≤–µ—В: EF=120
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т—Л—Б–Њ—В–∞ AH —А–Њ–Љ–±–∞ ABCD –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г CD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є DH=21 –Є CH=8. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —А–Њ–Љ–±–∞.
–Т—Л—Б–Њ—В–∞ AH —А–Њ–Љ–±–∞ ABCD –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г CD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є DH=21 –Є CH=8. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —А–Њ–Љ–±–∞.
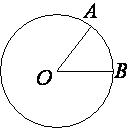 –Э–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –Њ—В–Љ–µ—З–µ–љ—Л —В–Њ—З–Ї–Є A –Є B —В–∞–Ї, —З—В–Њ ∠AOB=40¬∞. –Ф–ї–Є–љ–∞ –Љ–µ–љ—М—И–µ–є –і—Г–≥–Є AB —А–∞–≤–љ–∞ 50. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –±–Њ–ї—М—И–µ–є –і—Г–≥–Є.
–Э–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –Њ—В–Љ–µ—З–µ–љ—Л —В–Њ—З–Ї–Є A –Є B —В–∞–Ї, —З—В–Њ ∠AOB=40¬∞. –Ф–ї–Є–љ–∞ –Љ–µ–љ—М—И–µ–є –і—Г–≥–Є AB —А–∞–≤–љ–∞ 50. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –±–Њ–ї—М—И–µ–є –і—Г–≥–Є.
 –°—В–Њ—А–Њ–љ–∞ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ
∠C, –µ—Б–ї–Є ∠A=83¬∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–°—В–Њ—А–Њ–љ–∞ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ
∠C, –µ—Б–ї–Є ∠A=83¬∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 3, –∞ –Њ–і–Є–љ –Є–Ј –њ—А–Є–ї–µ–≥–∞—О—Й–Є—Е –Ї –љ–µ–є —Г–≥–ї–Њ–≤ —А–∞–≤–µ–љ 30¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –µ—Б–ї–Є –µ—С –Њ—Б–љ–Њ–≤–∞–љ–Є—П —А–∞–≤–љ—Л 2 –Є 6.
–С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 3, –∞ –Њ–і–Є–љ –Є–Ј –њ—А–Є–ї–µ–≥–∞—О—Й–Є—Е –Ї –љ–µ–є —Г–≥–ї–Њ–≤ —А–∞–≤–µ–љ 30¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –µ—Б–ї–Є –µ—С –Њ—Б–љ–Њ–≤–∞–љ–Є—П —А–∞–≤–љ—Л 2 –Є 6.
 –Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –љ–∞ –Ї–Њ—В–Њ—А–Њ–є –ї–µ–ґ–∞—В —В–Њ—З–Ї–Є A, B –Є C. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ ∠ABC=71¬∞ –Є ∠OAB=39¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї BCO. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –љ–∞ –Ї–Њ—В–Њ—А–Њ–є –ї–µ–ґ–∞—В —В–Њ—З–Ї–Є A, B –Є C. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ ∠ABC=71¬∞ –Є ∠OAB=39¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї BCO. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2018-11-23 22:20:48) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р–ї–µ–≤—В–Є–љ–∞, –µ—Б–ї–Є –Т—Л –Љ–Њ–ґ–µ—В–µ –њ—А–µ–і–ї–Њ–ґ–Є—В—М —А–µ—И–µ–љ–Є–µ –њ—А–Њ—Й–µ, –љ–∞–њ–Є—И–Є—В–µ –љ–∞–Љ, –±—Г–і–µ–Љ –Њ—З–µ–љ—М –±–ї–∞–≥–Њ–і–∞—А–љ—Л, –љ–µ —В–Њ–ї—М–Ї–Њ –Љ—Л, –љ–Њ –Є –≤—Б–µ –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї–Є. –Ь—Л –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –Њ–њ—Г–±–ї–Є–Ї—Г–µ–Љ –Т–∞—И–µ —А–µ—И–µ–љ–Є–µ –њ–Њ–і –Т–∞—И–Є–Љ –Є–Љ–µ–љ–µ–Љ.
(2018-11-21 22:48:47) –∞–ї–µ–≤—В–Є–љ–∞: –Т–Њ–њ—А–Њ—Б –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ: –њ–Њ—З–µ–Љ—Г –Њ—З–µ–љ—М –њ—А–Њ—Б—В—Г—О –Є –ї—С–≥–Ї—Г—О –Ј–∞–і–∞—З—Г, –Ї–Њ—В–Њ—А—Г—О –Љ–Њ–ґ–љ–Њ —А–µ—И–Є—В—М –≤ –і–≤–∞ –і–µ–є—Б—В–≤–Є—П, –Т—Л —А–µ—И–∞–µ—В–µ —Б–ї–Њ–ґ–љ–Њ –Є –љ–µ–Є–љ—В–µ—А–µ—Б–љ–Њ???
(2014-05-24 18:44:07) —В–∞–љ—О—И–Ї–∞: –Ш–і–µ–∞–ї—М–љ–Њ.