
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ430 –Η–Ζ 1087 |
 –î–≤–Β –Κ–Α―¹–Α―é―â–Η–Β―¹―è –≤–Ϋ–Β―à–Ϋ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β K –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, ―Ä–Α–¥–Η―É―¹―΄ –Κ–Ψ―²–Ψ―Ä―΄―Ö ―Ä–Α–≤–Ϋ―΄ 39 –Η 42, –≤–Ω–Η―¹–Α–Ϋ―΄ –≤ ―É–≥–Ψ–Μ ―¹ –≤–Β―Ä―à–Η–Ϋ–Ψ–Ι A. –û–±―â–Α―è –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è –Κ ―ç―²–Η–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―è–Φ, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É K, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―É–≥–Μ–Α –≤ ―²–Ψ―΅–Κ–Α―Ö B –Η C. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–î–≤–Β –Κ–Α―¹–Α―é―â–Η–Β―¹―è –≤–Ϋ–Β―à–Ϋ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β K –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, ―Ä–Α–¥–Η―É―¹―΄ –Κ–Ψ―²–Ψ―Ä―΄―Ö ―Ä–Α–≤–Ϋ―΄ 39 –Η 42, –≤–Ω–Η―¹–Α–Ϋ―΄ –≤ ―É–≥–Ψ–Μ ―¹ –≤–Β―Ä―à–Η–Ϋ–Ψ–Ι A. –û–±―â–Α―è –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è –Κ ―ç―²–Η–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―è–Φ, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É K, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―É–≥–Μ–Α –≤ ―²–Ψ―΅–Κ–Α―Ö B –Η C. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
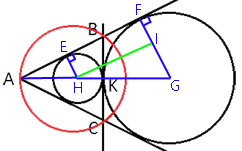 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ϋ–Β―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Ψ―²―Ä–Β–Ζ–Κ–Ψ–≤:
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ϋ–Β―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Ψ―²―Ä–Β–Ζ–Κ–Ψ–≤:
EH - ―Ä–Α–¥–Η―É―¹ –Φ–Α–Μ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η. –û–Ϋ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ AB (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι).
FG - ―Ä–Α–¥–Η―É―¹ –±–Ψ–Μ―¨―à–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η. –û–Ϋ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ AB (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι).
HG - –Ψ―²―Ä–Β–Ζ–Ψ–Κ, ―¹–Ψ–Β–¥–Η–Ϋ―è―é―â–Η–Ι ―Ü–Β–Ϋ―²―Ä―΄ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Β–Ι –Η ―Ä–Α–≤–Ϋ―΄–Ι R+r, ―²–Α–Κ –Κ–Α–Κ –Ψ–Ϋ –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É –ö.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η AFG –Η AEH:
∠EAH - –Ψ–±―â–Η–Ι;
―É–≥–Μ―΄ AEH –Η AFG - –Ω―Ä―è–Φ―΄–Β.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―ç―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η
–Ω–Ψ–¥–Ψ–±–Ϋ―΄, ―²–Ψ–≥–¥–Α:
FG/EH=AG/AH
FG/EH=(AH+HG)/AH
42/39=(AH+R+r)/AH
42AH=39(AH+81)
42AH-39AH=3159
AH=1053
sin∠EAH=EH/AH=39/1053=1/27
AK=AH+r=1053+39=1092
AK –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ BC, ―².–Κ. AK - ―ç―²–Ψ –Ω―Ä–Ψ–¥–Ψ–Μ–Ε–Β–Ϋ–Η–Β –±–Ψ–Μ―¨―à–Ψ–≥–Ψ –Η –Φ–Α–Μ–Ψ–≥–Ψ ―Ä–Α–¥–Η―É―¹–Ψ–≤, –Α BC -
–Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è –Κ –Φ–Α–Μ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η (
―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι). AK –¥–Β–Μ–Η―² ―Ö–Ψ―Ä–¥―É BC (BC - ―Ö–Ψ―Ä–¥–Α –¥–Μ―è –±–Ψ–Μ―¨―à–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η) –Ω–Ψ–Ω–Ψ–Μ–Α–Φ (–Ω–Ψ –≤―²–Ψ―Ä–Ψ–Φ―É
―¹–≤–Ψ–Ι―¹―²–≤―É ―Ö–Ψ―Ä–¥―΄).
–Δ―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC -
―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι, ―².–Κ. AK - –Η
–Φ–Β–¥–Η–Α–Ϋ–Α –Η
–≤―΄―¹–Ψ―²–Α (
―¹–≤–Ψ–Ι―¹―²–≤–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α).
–Δ–Β–Ω–Β―Ä―¨ ―É–±–Β―Ä–Β–Φ –Η–Ζ ―Ä–Η―¹―É–Ϋ–Κ–Α –≤―¹–Β, ―΅―²–Ψ –Ϋ–Α―¹ –±–Ψ–Μ―¨―à–Β –Ϋ–Β –Η–Ϋ―²–Β―Ä–Β―¹―É–Β―² –Η ―Ä–Β–Ζ―é–Φ–Η―Ä―É–Β–Φ, ―΅―²–Ψ –Φ―΄ –Ζ–Ϋ–Α–Β–Φ:
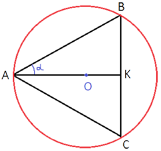 AK=1092
AK=1092
sinα=1/27
–Δ–Α–Κ –Κ–Α–Κ AK -
–±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α, ―²–Ψ ―Ü–Β–Ϋ―²―Ä –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –Ϋ–Α AK.
–ù–Α–Ι–¥–Β–Φ AB.
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
AB2=AK2+BK2
AB2=AK2+(AB*sinα)2
AB2-AB2*sin2α=10922
AB2(1-1/272)=10922
AB2(272-1)=272*10922
AB2=272*10922/(272-1)
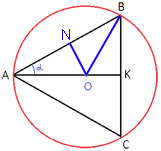 –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AOB.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AOB.
AO=OB, ―²–Α–Κ –Κ–Α–Κ ―ç―²–Ψ ―Ä–Α–¥–Η―É―¹―΄ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ
―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –≤―΄―¹–Ψ―²―É ON, –≤
―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –Ψ–Ϋ–Α ―²–Α–Κ –Ε–Β ―è–≤–Μ―è–Β―²―¹―è –Η
–Φ–Β–¥–Η–Α–Ϋ–Ψ–Ι (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α).
sinα=ON/AO => ON=AO/27
–ü–Ψ ―²–Β–Ψ―Ä–Β–Φ–Β
–ü–Η―³–Α–≥–Ψ―Ä–Α:
AO2=ON2+AN2
AO2=AO2/272+(AB/2)2
AO2((272-1)/272)=272*10922/(272-1)
–½–Α–Κ–Ψ–Ϋ―΅–Η–≤ –≤―¹–Β –≤―΄―΅–Η―¹–Μ–Β–Ϋ–Η―è, –Ω–Ψ–Μ―É―΅–Α–Β–Φ, ―΅―²–Ψ AO=546,75
–û―²–≤–Β―²: –†–Α–¥–Η―É―¹ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 546,75.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
–ö–Α–Κ–Η–Β –Η–Ζ –¥–Α–Ϋ–Ϋ―΄―Ö ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Ι –≤–Β―Ä–Ϋ―΄? –½–Α–Ω–Η―à–Η―²–Β –Η―Ö –Ϋ–Ψ–Φ–Β―Ä–Α.
1) –ù–Α –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η ―¹―É―â–Β―¹―²–≤―É–Β―² –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Α―è ―²–Ψ―΅–Κ–Α, ―Ä–Α–≤–Ϋ–Ψ―É–¥–Α–Μ―ë–Ϋ–Ϋ–Α―è –Ψ―² –Κ–Ψ–Ϋ―Ü–Ψ–≤ –Ψ―²―Ä–Β–Ζ–Κ–Α.
2) –£ –Μ―é–±–Ψ–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –Φ–Ψ–Ε–Ϋ–Ψ –≤–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨.
3) –ï―¹–Μ–Η –≤ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β –¥–≤–Β ―¹–Φ–Β–Ε–Ϋ―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Α–≤–Ϋ―΄, ―²–Ψ ―²–Α–Κ–Ψ–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ ―è–≤–Μ―è–Β―²―¹―è ―Ä–Ψ–Φ–±–Ψ–Φ.
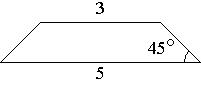 –£ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 3 –Η 5, –Α –Ψ–¥–Η–Ϋ –Η–Ζ ―É–≥–Μ–Ψ–≤ –Φ–Β–Ε–¥―É –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι –Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―Ä–Α–≤–Β–Ϋ 45¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–£ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 3 –Η 5, –Α –Ψ–¥–Η–Ϋ –Η–Ζ ―É–≥–Μ–Ψ–≤ –Φ–Β–Ε–¥―É –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι –Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―Ä–Α–≤–Β–Ϋ 45¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η.
 –£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AD=3, BC=1, –Α –Β―ë –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 12. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AD=3, BC=1, –Α –Β―ë –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 12. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–ü–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α
722√
 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2015-05-26 10:50:39) –î–Β–Ϋ–Η―¹: –· –Ϋ–Α―à–Β–Μ –Ψ―à–Η–±–Κ―É. –±–Μ–Η–Ε–Β –Κ –Κ–Ψ–Ϋ―Ü―É ―²–Α–Φ –¥–Ψ–Μ–Ε–Ϋ–Ψ –±―΄―²―¨ –ê–£ –Ω–Ψ–Ω–Ψ–Μ–Α–Φ, –Α –Ϋ–Β –Ω―Ä–Ψ―¹―²–Ψ.!!!
(2015-05-26 10:24:03) –†–Β―à–Β–Ϋ–Η–Β –Ϋ–Β –≤–Β―Ä–Ϋ–Ψ: –Ω―Ä–Η –Ϋ–Α―Ö–Ψ–Ε–¥–Β–Ϋ–Η–Η ―¹–Η–Ϋ―É―¹–Α ―É–≥–Μ–Α. –Ω―Ä–Ψ–≤–Β―Ä―¨―²–Β.
(2015-04-19 17:44:00) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –Δ–Α―²―¨―è–Ϋ–Α, –¥–Α, –Ϋ–Β –Ω―Ä–Η–≥–Ψ–¥–Η–Μ―¹―è ―ç―²–Ψ –Ψ―²―Ä–Β–Ζ–Ψ–Κ, –Η–Ζ–Ϋ–Α―΅–Α–Μ―¨–Ϋ–Ψ ―Ä–Β―à–Β–Ϋ–Η–Β –±―΄–Μ–Ψ –Ϋ–Β–Φ–Ϋ–Ψ–≥–Ψ –¥―Ä―É–≥–Η–Φ, –≥–¥–Β –Ψ–Ϋ –±―΄–Μ –Ϋ―É–Ε–Β–Ϋ...
(2015-04-19 14:09:59) –Δ–Α―²―¨―è–Ϋ–Α: –î–Μ―è ―΅–Β–≥–Ψ –±―΄–Μ –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ –Ψ―²―Ä–Β–Ζ–Ψ–Κ HI?
(2014-05-29 18:57:59) –ï–Κ–Α―²–Β―Ä–Η–Ϋ–Α: –Γ–Ω–Α―¹–Η–±–Ψ –±–Ψ–Μ―¨―à–Ψ–Β –Ζ–Α ―Ä–Β―à–Β–Ϋ–Η–Β