
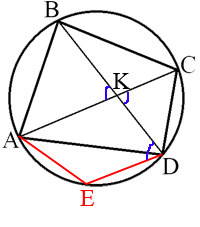
 Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Пусть R - радиус окружности.
Рассмотрим треугольник BCA.
Этот треугольник вписан в окружность, тогда по
теореме синусов:
AB/sin(∠BCA)=2R
AB=2Rsin(∠BCA)
Рассмотрим треугольник BCD.
Этот треугольник тоже вписан в окружность, тогда по
теореме синусов:
CD/sin(∠CBD)=2R
CD=2Rsin(∠CBD)
Рассмотрим треугольник BCK.
По
теореме о сумме углов треугольника:
∠CBD+∠BCA+∠CKB=180°
∠AKB - является смежным по отношению к ∠CKB, следовательно ∠CKB=180°-∠AKB. Подставляем в уравнение выше:
∠CBD+∠BCA+(180°-∠AKB)=180°
∠CBD+∠BCA+(180°-60°)=180°
∠CBD+∠BCA=60°
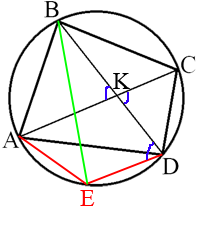 Для простоты обозначим ∠CBD=а и ∠BCA=b, т.е. a+b=60°
Для простоты обозначим ∠CBD=а и ∠BCA=b, т.е. a+b=60°
a=60°-b
19=AB=2Rsin(a)
22=CD=2Rsin(60°-a)=2R(sin60°cos(a)-cos60°sin(a))=2R((√
Разделим второе уравнение на первое:
19/22=R(√
19/22=(√
19*2sin(a)=22*(√
38sin(a)=22√
60sin(a)=22√
Возведем правую и левую части в квадрат:
3600sin2(a)=484*3cos2(a)
3600sin2(a)=1452(1-sin2(a)) (применена
основная тригонометрическая формула)
3600sin2(a)=1452-1452sin2(a))
5052sin2(a)=1452
sin2(a)=1452/5052
sin2(a)=484/1684
sin2(a)=121/421
sin(a)=√
sin(a)=11/√
22=2R*11/(√
1=R/(√
R=√
Ответ: R=√
Поделитесь решением
Присоединяйтесь к нам...
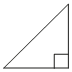 В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Комментарии: