Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Вариант №1 (предложил пользователь Всеволод).
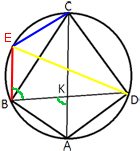Проведем BE||AC
ABCE - трапеция по
определению.
Так как эта
трапеция вписана в окружность, то данная
трапеция равнобедренная (по
свойству описанной окружности).
Следовательно EC=AB=19.
∠AKB=∠KBE=60°, т.к. это
накрест лежащие углы при параллельных прямых BE и AC.
BECD - четырехугольник, вписанный в окружность, следовательно:
∠ECD+∠KBE=180° (по
свойству).
∠ECD=180°-∠KBE=180°-60°=120°
Применим
теорему косинусов для треугольника CDE:
ED2=EC2+CD2-2*EC*CD*cos∠ECD
ED2=192+282-2*19*28*cos120°
ED2=361+784-2*19*28*(-1/2)
ED2=1145+532=1677
ED=√
А теперь применим
теорему синусов для треугольника CDE:
ED/sin∠ECD=2R
R=√
Ответ: R=√
Пусть R - радиус окружности.Поделитесь решением
Присоединяйтесь к нам...
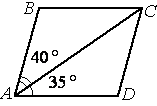Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
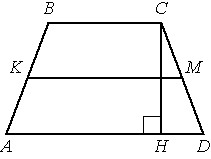В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
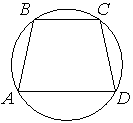Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: