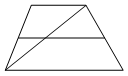
Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
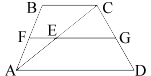Обозначим ключевые точки, как показано на рисунке.
Рассмотрим треугольник ABC.
AF=FB (по
определению средней линии трапеции).
Тогда, по теореме Фалеса:
AE=EC
Получается, что FE -
средняя линия треугольника ABC.
FE=BC/2=8/2=4 (по
теореме о средней линии треугольника).
Рассмотрим треугольник ACD.
Аналогично, EG -
средняя линия данного треугольника, следовательно EG=AD/2=18/2=9.
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
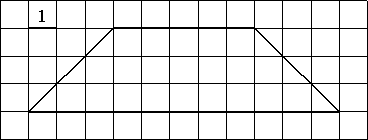Найдите площадь трапеции, изображённой на рисунке.
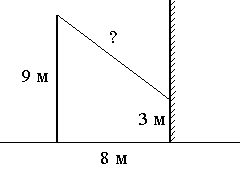От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: