Постройте график функции
x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Чтобы построить график функции состоящей из двух подфункций, необходимо построить график каждой подфункции на указанных для них диапазонах и объединить эти графики.
Так как в данном примере диапазоны обозначены неравенствами с
функцией модуля, то сначала решим эти неравенства:
Функция |x| всегда принимает положительные значения, и |x| будет меньше или равен 1, когда -1≤х≤1, т.е. x⊂[-1;1].
Следовательно |x|>1 на всем остальном пространстве, т.е. x⊂(-∞;-1)∪(1;+∞).
Запишем получившуюся функцию:
x2, если x⊂[-1;1]
1/x, если x⊂(-∞;-1)∪(1;+∞)
Построим по точкам график обоих подфункций в указанных диапазонах:
x2, если x⊂[-1;1]
| X | -1 | 0 | 1 |
| Y | 1 | 0 | 1 |
| X | -5 | -2 | -1 | 1 | 2 | 5 |
| Y | -0,2 | -0,5 | -1 | 1 | 0,5 | 0,2 |
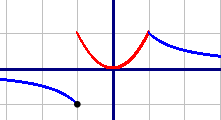График первой подфункции начерчен красным цветом, график второй подфункции - синим.
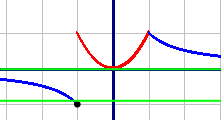Обратите внимание, что при с=0 прямая касается графика красной подфункции, а при всех остальных значениях - пересекает синюю подфункцию.Поделитесь решением
Присоединяйтесь к нам...
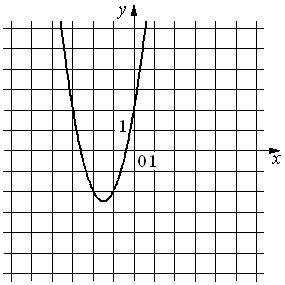На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-4;-2] 2) [-1;0] 3) [-2;-1] 4) [-2;0] |
Известно, что графики функций y=x2+p и y=2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=-x2-0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
Постройте график функции
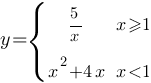и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Постройте график функции y=x2-4|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: