
Постройте график функции 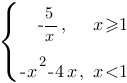 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Чтобы построить график этой функции, надо построить график каждой подфункции на указанных для подфункций диапазонах.
y1=-5/x на диапазоне [1;+∞)
y2=-x2-4x на диапазоне (-∞;1)
График первой подфункции - гипербола, будем строить его просто по точкам:
| X | 1 | 2 | 5 |
| Y | -5 | -2,5 | -1 |
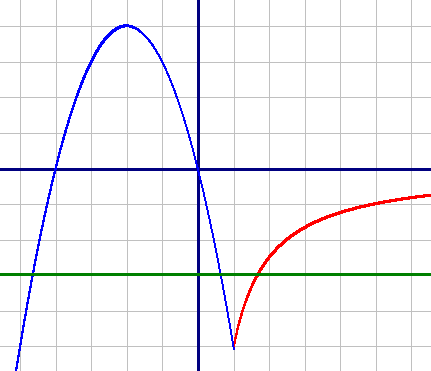 Красным цветом построен график первой подфункции y1=-5/x на диапазоне [1;+∞)
Красным цветом построен график первой подфункции y1=-5/x на диапазоне [1;+∞)Поделитесь решением
Присоединяйтесь к нам...
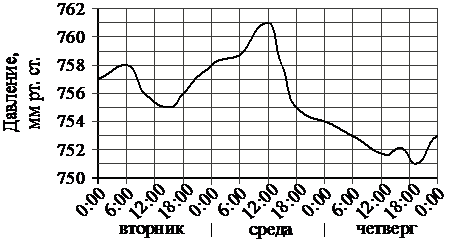 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по
вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления в четверг в 6 часов утра. Ответ дайте в мм рт. ст.
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по
вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления в четверг в 6 часов утра. Ответ дайте в мм рт. ст.
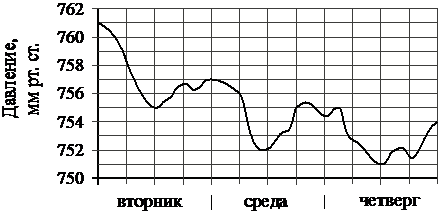 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b<0 Б) k>0, b>0 В) k<0, b>0
ГРАФИКИ
1)  2)
2)  3)
3) 
Постройте график функции 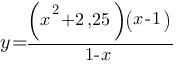 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Постройте график функции y=|x|(x+1)-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии: