Постройте график функции y=x2-5|x|+4. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
В данной функции присутствует
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=x2-5x+4, при x≥0
y=x2-5(-x)+4, при x<0
y=x2-5x+4, при x≥0
y=x2+5x+4, при x<0
Рассмотрим и построим график для каждой подфункции на определенном им диапазонах и объединим их.
График обеих подфункций - парабола, при чем, ветви параболы направлены вверх (так как коэффициент "а" больше нуля).
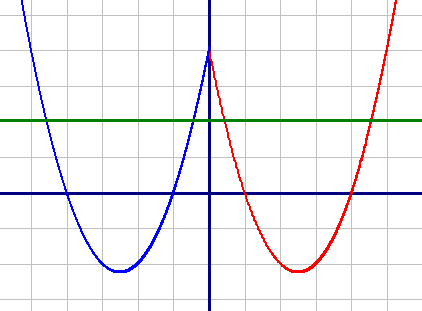Для первой подфункции (красная):
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 4 | 0 | -2 | -2 | 0 |
| X | 0 | -1 | -2 | -3 | -4 |
| Y | 4 | 0 | -2 | -2 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
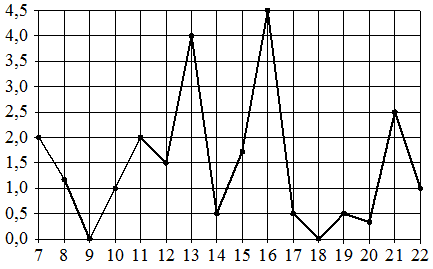На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки
на рисунке соединены линией. Определите по рисунку, какое наибольшее суточное количество осадков выпадало в Мурманске в данный период. Ответ дайте в миллиметрах.
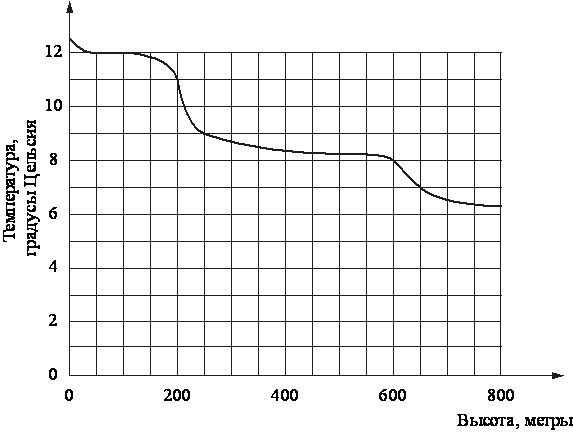На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
Определите по графику, на сколько градусов Цельсия температура на высоте 200 метров выше, чем на высоте 650 метров.
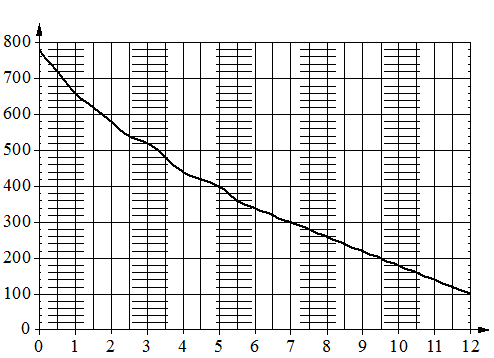На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 280 миллиметрам ртутного столба. Ответ дайте в километрах.
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=-2x+4
Б) y=2x-4
В) y=2x+4
ГРАФИКИ
1) 
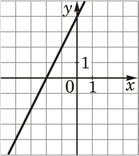2) 
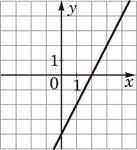3) 
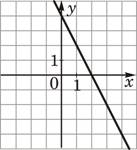
В таблице под каждой буквой укажите соответствующий номер.
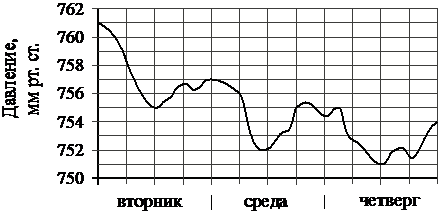На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления (в мм рт. ст.) в среду в 18 часов вечера. Ответ дайте в мм рт. ст.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: