Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
x*x+x-6x, при x≥0
(-x)x+(-x)-6x, при x<0
x2-5x, при x≥0
-x2-7x, при x<0
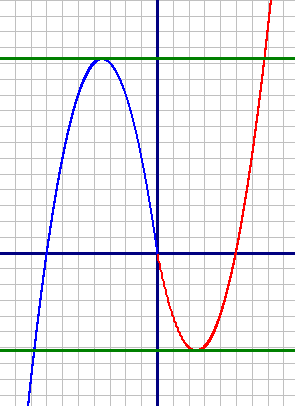Обе подфункции - параболы. Построим их по точкам:
y1=x2-5x (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -4 | -6 | -6 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 6 | 10 | 12 |
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения (x+5)2-x(x-10) при x=-1/20.
Закон всемирного тяготения можно записать в виде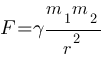 
, где F — сила притяжения между телами (в ньютонах), m1 и m2 — массы тел (в килограммах), r — расстояние между центрами масс тел (в метрах), а γ — гравитационная постоянная, равная 6,67*10-11 Н*м2/кг2. Пользуясь этой формулой, найдите массу тела m1 (в килограммах), если F=0,64032 Н, m2=4*109 кг, а r=5 м.
Постройте график функции
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Найдите значение выражения (6-c)2-c(c+3) при c=-1/15.
Найдите значение выражения 
при a=9,2.
Хочу получать новые решения
Ни какого спама
Автор: Таська
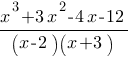
Комментарии: