Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Рассмотрим каждое утверждение.
1) В тупоугольном треугольнике все углы тупые.
Тупой угол - это угол больше 90°. Если утверждение верно, то сумма углов тупоугольного треугольника будет дольше 270°. А это не верно, т.к. противоречит теореме о сумме углов треугольника. Утверждение неверно.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам. Это утверждение верно, т.к. это свойство параллелограмма.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка. Это утверждение верно, т.к. это свойство серединного перпендикуляра (другое название - медиатрисса).
Ответ: 2), 3)
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
Площадь прямоугольного треугольника равна 512√
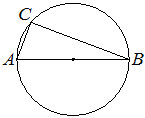Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
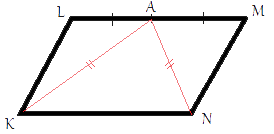В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: