
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Рассмотрим треугольники ADC и CBD.
 ∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠CDB - общий для обоих треугольников, следовательно, по
признаку подобия, треугольники ADC и CBD -
подобны.
Следовательно, по определению подобных треугольников запишем:
CD/BD=AC/BC=AD/CD
AC/BC=AM/MB=7/9 (по первому
свойству биссектрисы).
Получаем, что:
AD/CD=7/9
AD=CD*7/9
И...
CD/BD=7/9
9CD=7BD
BD=CD*9/7
BD=AD+AB=AD+9+7=AD+16
AD+16=CD*9/7
Подставляем значение AD, которое получили ранее AD=CD*7/9
CD*7/9+16=CD*9/7
16=CD*9/7-CD*7/9
Приводим к общему знаменателю:
16=(9*9*CD-7*7*CD)/(7*9)
16=(81CD-49CD)/63
16*63=81CD-49CD
16*63=32CD
CD=16*63/32=63/2=31,5
Ответ: CD=31,5
Поделитесь решением
Присоединяйтесь к нам...
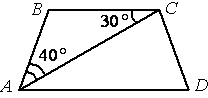 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
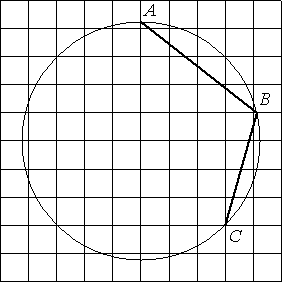 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
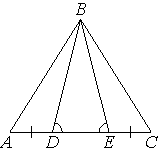 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
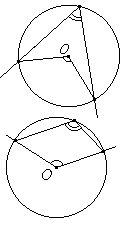 Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.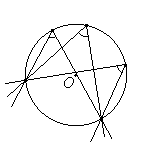 Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.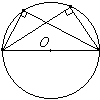 Вписанный угол, опирающийся на диаметр, равен 90°.
Вписанный угол, опирающийся на диаметр, равен 90°.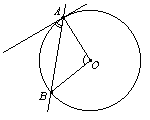 Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Комментарии: