
Решите неравенство 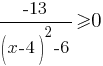
Посмотрим внимательно на неравенство. Числитель дроби - это отрицательное число. Эта дробь ни при каком "х" не будет равной нулю, так как раной нулю она станет только тогда, когда числитель будет равен нулю. А это невозможно, так как числитель у нас равен -13. Следовательно, это нестрогое неравенство можно записать как строгое:

Далее, так как числитель отрицательный, то эта дробь будет больше нуля только тогда, когда знаменатель тоже будет отрицательным (минус на минус даст плюс).Следовательно, нам достаточно найти при каких значениях "х" знаменатель будет отрицательным - это и будет решением неравенства:
(x-4)2-6<0
Раскроем скобки по формуле
квадрат разности:
x2-2*x*(-4)+42-6<0
x2+8x+16-6<0
x2+8x+10<0
 Это квадратичная функция, следовательно ее график - парабола. Коэффициент "а" (коэффициент при x2) равен 1, т.е. больше нуля, то ветви параболы направлены вверх.
Это квадратичная функция, следовательно ее график - парабола. Коэффициент "а" (коэффициент при x2) равен 1, т.е. больше нуля, то ветви параболы направлены вверх.
Значение это функции меньше нуля, когда график располагается ниже оси Х. Следовательно, надо найти корни квадратного уравнения через
дискриминант:
x2+8x+10=0
D=82-4*1*10=64-40=24
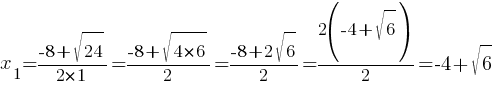
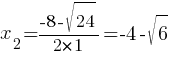
Еще раз, значение функции будет меньше нуля, когда х принадлежит диапазону от x1 до x2:
Ответ: x∈(-4-√6 ; -4+√6)
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение x6=(7x-12)3.
Решите уравнение x+2-4(x-2)=5(3-x)+3.
Решите неравенство 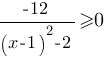
Решите неравенство 9x-4(2x+1)>-8.
1) (-4;+∞)
2) (-12;+∞)
3) (-∞;-4)
4) (-∞;-12)
Решите уравнение (x+5)3=25(x+5).
Комментарии: