Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
Введем обозначения:
v - скорость первого автомобилиста.
v-11 - скорость второго автомобилиста на первой половине пути.
S - длина пути из А в В.
S/v - время в пути первого автомобилиста.
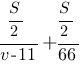- время в пути второго автомобилиста.
Время в пути для обоих автомобилистов одно и то же, так как они одновременно выехали и одновременно приехали, следовательно, можем записать:
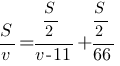
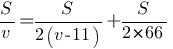
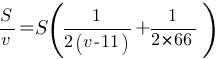сокращаем S
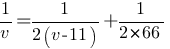
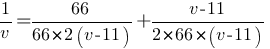
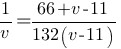
132(v-11)=v(55+v)
132v-1452=55v+v2
0=55v+v2-132v+1452
v2-77v+1452=0
Решим это
квадратное уравнение через
дискриминант:
D=(-77)2-4*1*1452=5929-5808=121
v1=(-(-77)+11)/(2*1)=(77+11)/2=88/2=44 км/ч
v2=(-(-77)-11)/(2*1)=(77-11)/2=66/2=33 км/ч
По условию задачи, скорость первого автомобилиста больше 40км/ч, значит подходит только 44 км/ч.
Ответ: 44
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение x3+5x2-x-5=0.
На координатной прямой отмечено число a.
Расположите в порядке убывания числа a-1, 1/a, a.
1) a-1, 1/a, a
2) 1/a, a, a-1
3) 1/a, a-1, a
4) a, 1/a, a-1
На каком рисунке изображено множество решений системы неравенств
x<8
9-x<0?
1) система не имеет решений
2) 
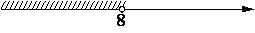
3) 
4) 
Решите неравенство 3x-x2>0.
Решите неравенство 2x-x2<0.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: