
Решите уравнение (x+2)4-4(x+2)2-5=0.
Введем обозначение:
t=(x+2)2
Тогда получаем уравнение:
t2-4t-5=0
Решим это квадратное уравнение через
дискриминант:
D=(-4)2-4*1*(-5)=16+20=36
t1=(-(-4)+6)/(2*1)=(4+6)/2=5
t2=(-(-4)-6)/(2*1)=(4-6)/2=-1
Теперь найдем "х" из параметра "t", для этого по очереди подставим оба значения "t":
1) t=5
(x+2)2=5
Можно пойти по быстрому пути решения этого уравнения:
Извлечем квадратный корень из правой и левой частей, получим:
x+2=±√5
x1=-2+√5
x2=-2-√5
Для тех, что не понял этот метод, пойдем по пути решения через дискриминант.
Для этого раскроем скобку (x+2)2 по формуле
квадрат разности, получаем:
x2+2*x*2+22=5
x2+4x+4-5=0
x2+4x-1=0
D=42-4*1*(-1)=16+4=20
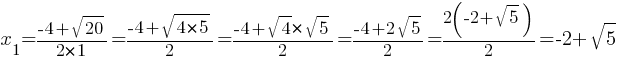
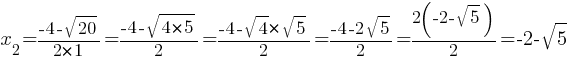
Естественно, мы получили тот же результат.
2) t=-1
(x+2)2=-1
Это уравнение не имеет решений, так как квадрат любого числа дает положительный результат и никак не может равняться -1.
Ответ: x1=-2+√5, x2=-2-√5
Поделитесь решением
Присоединяйтесь к нам...
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
На каком рисунке изображено множество решений неравенства
3-4x>11-8(x-2)?
1) 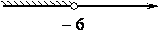
2) 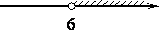
3) 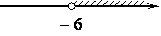
4) 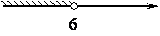
Найдите наименьшее значение x, удовлетворяющее системе неравенств
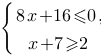
Решите неравенство:
14/(x2+2x-15)≤0
.
Решите неравенство (x-7)2<√
Комментарии: