Из пункта А в пункт В, расстояние между которыми 27 км, вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что она была на 2 км/ч меньше скорости пешехода.
Введем обозначения:
vт - скорость туриста
vт+2 - скорость пешехода
tт - время туриста в пути
tт-0,5 - время пешехода в пути
Турист прошел 12 км.
Пешеход прошел 27-12=15 км.
Запишем соответствующие уравнения:
12=vт*tт
15=(vт+2)(tт-0,5)
12=vт*tт
15=vт*tт-0,5vт+2tт-2*0,5
Так как vт*tт=15, то сразу подставим это значение:
12=vт*tт
15=12-0,5vт+2tт-1
12=vт*tт
15-12+1=-0,5vт+2tт
12/vт=tт
4=-0,5vт+2tт
12/vт=tт
4=-0,5vт+2*12/vт
Решим второе уравнение:
4=-0,5vт+2*12/vт |*vт
4vт=-0,5v2т+24
0,5v2т+4vт-24=0
Решим это квадратное уравнение через дискриминант:
D=42-4*0,5*(-24)=16+48=64
vт1=(-4+8)/(2*0,5)=4/1=4
vт2=(-4-8)/(2*0,5)=-12/1=-12
Так как скорость отрицательной быть не может, то vт=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
На каком рисунке изображено множество решений системы неравенств
x>-1,
-4-x>0?
1) 
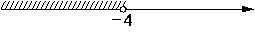
2) 
3) 
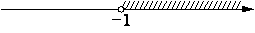
4) система не имеет решений
Решите уравнение 10x+9=7x.
Известно, что a и b — положительные числа и a>b. Сравните 1/a и 1/b.
На координатной прямой отмечено число c. Расположите в порядке убывания числа c, c2 и 1/c.
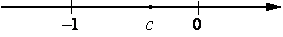
Два автомобиля одновременно отправляются в 560-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: