
Решите уравнение x3+5x2-9x-45=0.
x3+5x2-9x-45=0
Из первых двух членов уравнения вынесем за скобки x2:
x2(x+5)-9x-45=0
Из остальных членов вынесем "-9":
x2(x+5)-9(x+5)=0
Теперь вынесем за общую скобку (x+5):
(x+5)(x2-9)=0
Во второй скобке воспользуемся формулой
разность квадратов:
(x+5)(x2-32)=0
(x+5)(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю. У нас три множителя, поэтому рассмотрим 3 случая:
1) x+5=0 => x1=-5
2) x-3=0 => x2=3
3) x+3=0 => x3=-3
Ответ: x1=-5, x2=3, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
За 6 минут велосипедист проехал a километров. Сколько километров он проедет за 35 минут, если будет ехать с той же скоростью? Запишите соответствующее выражение.
В какое из следующих выражений можно преобразовать дробь 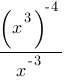 ?
?
1) x-9
2) x-15
3) x4
4) x2
Найдите значение выражения 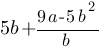 при a=-76, b=76.
при a=-76, b=76.
Решите уравнение x2-6x+√
Найдите значение выражения (6,8*10-2)(8*10-4).
Комментарии: