
Решите уравнение (x2-25)2+(x2+2x-15)2=0.
Можно попробовать раскрыть скобки, мы получим уравнение четверной степени, решение которого может быть довольно сложным. Поэтому предлагается два других варианта решения.
Вариант №1 (предложил пользователь Людмила)
Внимательно посмотрим на уравнение. Оно представляет из себя сумму квадратов равных нулю. Квадрат любого числа положителен. Следовательно, сумма квадратов равна нулю, когда каждый квадрат равен нулю. Получается система уравнений:
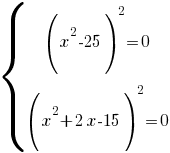
Так как квадрат равен нулю, то и число под квадратом равно нулю:
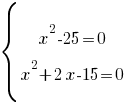
Осталось решить каждое уравнение по отдельности, и корень, который удовлетворяет обоим уравнениям, и будет решением системы.
1) x2-25=0
x2-52=0
Воспользуемся формулой разность квадратов:
(x-5)(x+5)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому:
x1=5
x2=-5
Это корни первого уравнения.
2) x2+2x-15=0
Найдем корни этого квадратного уравнения через дискриминант:
D=22-4*1*(-15)=4+60=64
x1=(-2+8)/(2*1)=6/2=3
x2=(-2-8)/(2*1)=-10/2=-5
Это корни второго уравнения.
Для обоих уравнений есть общий корень x=-5. Это и есть решение системы уравнений и решение первоначального уравнения.
Ответ: -5
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=|x|(x-1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
При каких значениях р вершины парабол у=х2+4рх-1 и у=-х2+6рх-р расположены по разные стороны от оси х?
Найдите значение выражения √
Найдите значение выражения 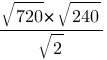
1) 120√
2) 240√
3) 360√
4) 120√
Найдите значение выражения (x-5)2-x(10+x) при x=-1/20.
Комментарии:
(2018-10-09 12:01:40) Администратор: Людмила, Вы правы, я обязательно добавлю такой вариант решения.
(2018-10-09 11:57:52) Людмила: Почему не решаете уравнение проще? Сумма квадратов равна 0 только тогда, когда каждое слагаемое равно 0. Получаем систему уравнений.