Решите уравнение x3+5x2-9x-45=0.
x3+5x2-9x-45=0
x2(x+5)-9(x+5)=0
Вынесем (x+5) за общую скобку:
(x+5)(x2-9)=0
(x+5)(x2-32)=0
Для второй скобки воспользуемся формулой разность квадратов:
(x+5)(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому приравняем каждую скобку к нулю:
1) x+5=0 => x1=-5
2) x-3=0 => x2=3
3) x+3=0 => x3=-3
Ответ: x1=-5, x2=3, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения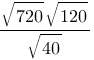 
1) 60√
2) 12√
3) 12√
4) 36√
Значение какого выражения является рациональным числом?
1) (√
2) 3√
3) √
4) √
Значение какого из выражений является числом иррациональным?
1) √
2) (√
3) √
4) √
Парабола проходит через точки K(0;-5), L(4;3), M(-3;10). Найдите координаты её вершины.
Найдите значение выражения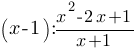 
при x=-99.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-12-06 18:10:04) Администратор: Инна, я расписал решение немного подробней. Надеюсь стало понятней.
(2017-12-06 17:59:12) Инна : А как найти икс первое икс второе и икс третье
(2017-12-06 17:50:40) Инна: Как нашли х1,х2,х3??