Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Рассмотрим каждое утверждение.
1) В тупоугольном треугольнике все углы тупые.
Тупой угол - это угол больше 90°. Если утверждение верно, то сумма углов тупоугольного треугольника будет дольше 270°. А это не верно, т.к. противоречит теореме о сумме углов треугольника. Утверждение неверно.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам. Это утверждение верно, т.к. это свойство параллелограмма.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка. Это утверждение верно, т.к. это свойство серединного перпендикуляра (другое название - медиатрисса).
Ответ: 2), 3)
Поделитесь решением
Присоединяйтесь к нам...
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
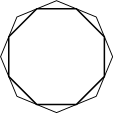Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
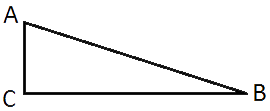Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: