
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ551 –ł–∑ 1087 |
 –Ě–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ BC –ĺ—Ā—ā—Ä–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC (AB≠AC) –ļ–į–ļ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–į –Ņ–ĺ–Ľ—É–ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–į—Ź –≤—č—Ā–ĺ—ā—É AD –≤ —ā–ĺ—á–ļ–Ķ M, AD=27, MD=18, H ‚ÄĒ —ā–ĺ—á–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –≤—č—Ā–ĺ—ā —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –Ě–į–Ļ–ī–ł—ā–Ķ AH.
–Ě–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ BC –ĺ—Ā—ā—Ä–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC (AB≠AC) –ļ–į–ļ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–į –Ņ–ĺ–Ľ—É–ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–į—Ź –≤—č—Ā–ĺ—ā—É AD –≤ —ā–ĺ—á–ļ–Ķ M, AD=27, MD=18, H ‚ÄĒ —ā–ĺ—á–ļ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –≤—č—Ā–ĺ—ā —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –Ě–į–Ļ–ī–ł—ā–Ķ AH.
–í–į—Ä–ł–į–Ĺ—ā 1 –ü—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ –ź–Ĺ–ī—Ä–Ķ–Ļ –°–Ķ—Ä–Ķ–ī–Ĺ–ł–ļ–ĺ–≤
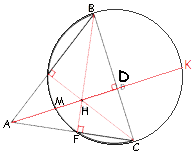 –Ē–ĺ—Ä–ł—Ā—É–Ķ–ľ –Ņ–ĺ–Ľ—É–ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ī–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–Ē–ĺ—Ä–ł—Ā—É–Ķ–ľ –Ņ–ĺ–Ľ—É–ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ī–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–ü—Ä–ĺ–ī–Ľ–ł–ľ
–≤—č—Ā–ĺ—ā—É AD –ī–ĺ –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź —Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć—é, –ĺ–Ī–ĺ–∑–Ĺ–į—á–ł–ľ —ā–ĺ—á–ļ—É –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ö.
–ě–Ī–ĺ–∑–Ĺ–į—á–ł–ľ F –ļ–į–ļ —ā–ĺ—á–ļ—É –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ł —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AC.
BF - —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź
–≤—č—Ā–ĺ—ā–ĺ–Ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, —ā–į–ļ –ļ–į–ļ –ī–Ľ—Ź –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł ∠BFC -
–≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–Ļ —É–≥–ĺ–Ľ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į –ī—É–≥—É –≤ 180¬į (BC - –ī–ł–į–ľ–Ķ—ā—Ä), —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ ∠BFC=180¬į/2=90¬į
1) AF*AC=AM*AK (–Ņ–ĺ
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ –ī–≤—É—Ö —Ā–Ķ–ļ—É—Č–ł—Ö).
2) –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ
—Ö–ĺ—Ä–ī—É MK.
BC - –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä –ļ MK, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–ł–Ļ —á–Ķ—Ä–Ķ–∑ —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ BC -
—Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–Ĺ—č–Ļ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä.
–≠—ā–ĺ –∑–Ĺ–į—á–ł—ā, BC –ī–Ķ–Ľ–ł—ā
—Ö–ĺ—Ä–ī—É MK –Ņ–ĺ–Ņ–ĺ–Ľ–į–ľ, —ā.–Ķ. MD=KD=18
3) –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł AHF –ł ACD.
∠DAC - –ĺ–Ī—Č–ł–Ļ.
∠AFH=∠ADC - —ć—ā–ĺ –Ņ—Ä—Ź–ľ—č–Ķ —É–≥–Ľ—č.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ņ–ĺ
–Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤, –ī–į–Ĺ–Ĺ—č–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–Ę–ĺ–≥–ī–į, –Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é
–Ņ–ĺ–ī–ĺ–Ī–ł—Ź, –ľ—č –ľ–ĺ–∂–Ķ–ľ –∑–į–Ņ–ł—Ā–į—ā—Ć:
AC/AH=AD/AF => AC*AF=AD*AH
–í –Ņ. 1) –ľ—č –Ņ–ĺ–Ľ—É—á–ł–Ľ–ł —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ AF*AC=AM*AK, —ā–ĺ–≥–ī–į:
AM*AK=AD*AH
AH=AM*AK/AD
–ė–∑ —Ä–ł—Ā—É–Ĺ–ļ–į –Ĺ–į—Ö–ĺ–ī–ł–ľ:
AM=AD-MD=27-18=9
AK=AD+KD=27+18=45
–Ę–ĺ–≥–ī–į:
AH=9*45/27=45/3=15
–ě—ā–≤–Ķ—ā: AH=15
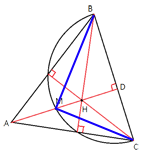 –ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –ĺ—ā—Ä–Ķ–∑–ļ–ł CM –ł MB.
–ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –ĺ—ā—Ä–Ķ–∑–ļ–ł CM –ł MB.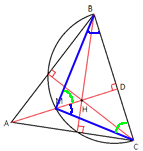 –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł MBC –ł MD–°.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł MBC –ł MD–°.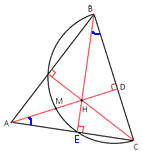 –í–Ķ—Ä–Ĺ–Ķ–ľ—Ā—Ź –ļ –Ņ–Ķ—Ä–≤–ĺ–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–ľ—É —Ä–ł—Ā—É–Ĺ–ļ—É –ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł AHE –ł BHD.
–í–Ķ—Ä–Ĺ–Ķ–ľ—Ā—Ź –ļ –Ņ–Ķ—Ä–≤–ĺ–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–ľ—É —Ä–ł—Ā—É–Ĺ–ļ—É –ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł AHE –ł BHD.–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā—č —É–≥–Ľ–ĺ–≤ A –ł B –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BC=2, –į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł K –ī–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB —Ä–į–≤–Ĺ–ĺ 1.
–Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā—č —É–≥–Ľ–ĺ–≤ A –ł B –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BC=2, –į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł K –ī–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB —Ä–į–≤–Ĺ–ĺ 1.
 –Ě–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ –ź–° —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ź–í–° –≤—č–Ī—Ä–į–Ĺ—č —ā–ĺ—á–ļ–ł D –ł E —ā–į–ļ, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł AD –ł CE —Ä–į–≤–Ĺ—č (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –ě–ļ–į–∑–į–Ľ–ĺ—Ā—Ć, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł BD –ł BE —ā–ĺ–∂–Ķ —Ä–į–≤–Ĺ—č. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ź–í–° ‚ÄĒ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
–Ě–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ –ź–° —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ź–í–° –≤—č–Ī—Ä–į–Ĺ—č —ā–ĺ—á–ļ–ł D –ł E —ā–į–ļ, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł AD –ł CE —Ä–į–≤–Ĺ—č (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –ě–ļ–į–∑–į–Ľ–ĺ—Ā—Ć, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł BD –ł BE —ā–ĺ–∂–Ķ —Ä–į–≤–Ĺ—č. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ź–í–° ‚ÄĒ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
 –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–ĺ–ľ–Ī–į, –Ķ—Ā–Ľ–ł –Ķ–≥–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł —Ä–į–≤–Ĺ—č 39 –ł 2.
–Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–ĺ–ľ–Ī–į, –Ķ—Ā–Ľ–ł –Ķ–≥–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł —Ä–į–≤–Ĺ—č 39 –ł 2.
 –í –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į —Ä–į–≤–Ĺ–į 70, –į –ĺ–ī–ł–Ĺ –ł–∑ –ĺ—Ā—ā—Ä—č—Ö —É–≥–Ľ–ĺ–≤ —Ä–į–≤–Ķ–Ĺ 45¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
–í –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į —Ä–į–≤–Ĺ–į 70, –į –ĺ–ī–ł–Ĺ –ł–∑ –ĺ—Ā—ā—Ä—č—Ö —É–≥–Ľ–ĺ–≤ —Ä–į–≤–Ķ–Ĺ 45¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
 –í –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į —Ä–į–≤–Ĺ–į 70, –į –ĺ–ī–ł–Ĺ –ł–∑ –ĺ—Ā—ā—Ä—č—Ö —É–≥–Ľ–ĺ–≤ —Ä–į–≤–Ķ–Ĺ 45¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
–í –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į —Ä–į–≤–Ĺ–į 70, –į –ĺ–ī–ł–Ĺ –ł–∑ –ĺ—Ā—ā—Ä—č—Ö —É–≥–Ľ–ĺ–≤ —Ä–į–≤–Ķ–Ĺ 45¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2016-12-08 19:09:59) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –ģ–Ľ–ł—Ź, –ú—č –Ĺ–Ķ –Ņ–ĺ–ľ–ĺ–≥–į–Ķ–ľ —Ä–Ķ—ą–ł—ā—Ć –ī–ĺ–ľ–į—ą–Ĺ–Ķ–Ķ –∑–į–ī–į–Ĺ–ł–Ķ, —Ü–Ķ–Ľ—Ć —Ā–į–Ļ—ā–į - –Ņ–ĺ–ī—Ä–ĺ–Ī–Ĺ–ĺ —Ä–į–∑–ĺ–Ī—Ä–į—ā—Ć –∑–į–ī–į—á–ł, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ī—É–ī—É—ā –Ĺ–į —ć–ļ–∑–į–ľ–Ķ–Ĺ–į—Ö, —á—ā–ĺ–Ī—č —É—á–į—Č–ł–Ķ—Ā—Ź –Ĺ–į—É—á–ł–Ľ–ł—Ā—Ć –ł—Ö —Ä–Ķ—ą–į—ā—Ć —Ā–į–ľ–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ. –ē—Ā–Ľ–ł –Ĺ–į–Ļ–ī–Ķ—ā–Ķ –Ņ–ĺ—Ö–ĺ–∂—É—é –∑–į–ī–į—á—É –Ĺ–į —Ā–į–Ļ—ā–Ķ fipi.ru, –Ņ–ł—ą–ł—ā–Ķ, –ĺ–Ī—Ź–∑–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ī–ĺ–Ī–į–≤–ł–ľ.
(2016-12-08 15:19:31) –ģ–Ľ–ł—Ź : –Ě–į –Ī–ĺ–ļ–ĺ–≤—č—Ö —Ā—ā–ĺ—Ä–ĺ–Ĺ–į—Ö —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ź–í–° –ĺ—ā–Ľ–ĺ–∂–Ķ–Ĺ—č —Ä–į–≤–Ĺ—č–Ķ –ĺ—ā—Ä–Ķ–∑–ļ–ł –ź–ú –ł –ź–ö. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –í–°–ú=—ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ—É–°–í–ö.
(2015-02-14 16:05:23) –Ē–Ķ–Ĺ–ł—Ā: –ú–ĺ–≥—É —Ā–ļ–ł–Ĺ—É—ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ: ppepsicola@mail.ru (–∑–į—Ö–ĺ–∂—É –Ĺ–Ķ –ļ–į–∂–ī—č–Ļ –ī–Ķ–Ĺ—Ć)
(2015-02-14 16:04:36) –Ē–Ķ–Ĺ–ł—Ā:: —Ä–Ķ—ą–į–Ľ –Ĺ–Ķ–ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–ī—Ä—É–≥–ĺ–ľ—É, –Ņ–ĺ–Ľ—É—á–ł–Ľ–ĺ—Ā—Ć 22,5