
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ750 –Є–Ј 1087 |
 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=19 –Є CD=28 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=19 –Є CD=28 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Т–∞—А–Є–∞–љ—В вДЦ1 (–њ—А–µ–і–ї–Њ–ґ–Є–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Т—Б–µ–≤–Њ–ї–Њ–і).
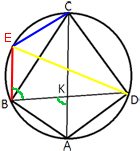 –Я—А–Њ–≤–µ–і–µ–Љ BE||AC
–Я—А–Њ–≤–µ–і–µ–Љ BE||AC
ABCE - —В—А–∞–њ–µ—Ж–Є—П –њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О.
–Ґ–∞–Ї –Ї–∞–Ї —Н—В–∞
—В—А–∞–њ–µ—Ж–Є—П –≤–њ–Є—Б–∞–љ–∞ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —В–Њ –і–∞–љ–љ–∞—П
—В—А–∞–њ–µ—Ж–Є—П —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–∞—П (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ EC=AB=19.
∠AKB=∠KBE=60¬∞, —В.–Ї. —Н—В–Њ
–љ–∞–Ї—А–µ—Б—В –ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л –њ—А–Є –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ—А—П–Љ—Л—Е BE –Є AC.
BECD - —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї, –≤–њ–Є—Б–∞–љ–љ—Л–є –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ:
∠ECD+∠KBE=180¬∞ (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г).
∠ECD=180¬∞-∠KBE=180¬∞-60¬∞=120¬∞
–Я—А–Є–Љ–µ–љ–Є–Љ
—В–µ–Њ—А–µ–Љ—Г –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ CDE:
ED2=EC2+CD2-2*EC*CD*cos∠ECD
ED2=192+282-2*19*28*cos120°
ED2=361+784-2*19*28*(-1/2)
ED2=1145+532=1677
ED=√
–Р —В–µ–њ–µ—А—М –њ—А–Є–Љ–µ–љ–Є–Љ
—В–µ–Њ—А–µ–Љ—Г —Б–Є–љ—Г—Б–Њ–≤ –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ CDE:
ED/sin∠ECD=2R
R=√
–Ю—В–≤–µ—В: R=√
 –Я—Г—Б—В—М R - —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–Я—Г—Б—В—М R - —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
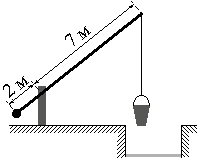 –Э–∞ —А–Є—Б—Г–љ–Ї–µ –Є–Ј–Њ–±—А–∞–ґ—С–љ –Ї–Њ–ї–Њ–і–µ—Ж —Б ¬Ђ–ґ—Г—А–∞–≤–ї—С–Љ¬ї. –Ъ–Њ—А–Њ—В–Ї–Њ–µ –њ–ї–µ—З–Њ –Є–Љ–µ–µ—В –і–ї–Є–љ—Г 2 –Љ, –∞ –і–ї–Є–љ–љ–Њ–µ –њ–ї–µ—З–Њ вАФ 7 –Љ. –Э–∞ —Б–Ї–Њ–ї—М–Ї–Њ –Љ–µ—В—А–Њ–≤ –Њ–њ—Г—Б—В–Є—В—Б—П –Ї–Њ–љ–µ—Ж –і–ї–Є–љ–љ–Њ–≥–Њ –њ–ї–µ—З–∞, –Ї–Њ–≥–і–∞ –Ї–Њ–љ–µ—Ж –Ї–Њ—А–Њ—В–Ї–Њ–≥–Њ –њ–Њ–і–љ–Є–Љ–µ—В—Б—П –љ–∞ 1 –Љ?
–Э–∞ —А–Є—Б—Г–љ–Ї–µ –Є–Ј–Њ–±—А–∞–ґ—С–љ –Ї–Њ–ї–Њ–і–µ—Ж —Б ¬Ђ–ґ—Г—А–∞–≤–ї—С–Љ¬ї. –Ъ–Њ—А–Њ—В–Ї–Њ–µ –њ–ї–µ—З–Њ –Є–Љ–µ–µ—В –і–ї–Є–љ—Г 2 –Љ, –∞ –і–ї–Є–љ–љ–Њ–µ –њ–ї–µ—З–Њ вАФ 7 –Љ. –Э–∞ —Б–Ї–Њ–ї—М–Ї–Њ –Љ–µ—В—А–Њ–≤ –Њ–њ—Г—Б—В–Є—В—Б—П –Ї–Њ–љ–µ—Ж –і–ї–Є–љ–љ–Њ–≥–Њ –њ–ї–µ—З–∞, –Ї–Њ–≥–і–∞ –Ї–Њ–љ–µ—Ж –Ї–Њ—А–Њ—В–Ї–Њ–≥–Њ –њ–Њ–і–љ–Є–Љ–µ—В—Б—П –љ–∞ 1 –Љ?
 –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –≤ —В–Њ—З–Ї–∞—Е K –Є P —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Є –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –≤–µ—А—И–Є–љ—Л B –Є C. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ KP, –µ—Б–ї–Є AP=18, –∞ —Б—В–Њ—А–Њ–љ–∞ BC –≤ 1,2 —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ —Б—В–Њ—А–Њ–љ—Л AB.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –≤ —В–Њ—З–Ї–∞—Е K –Є P —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Є –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –≤–µ—А—И–Є–љ—Л B –Є C. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ KP, –µ—Б–ї–Є AP=18, –∞ —Б—В–Њ—А–Њ–љ–∞ BC –≤ 1,2 —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ —Б—В–Њ—А–Њ–љ—Л AB.
 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–∞–њ–µ—Ж–Є—О, —А–∞–≤–µ–љ 48. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–∞–њ–µ—Ж–Є—О, —А–∞–≤–µ–љ 48. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
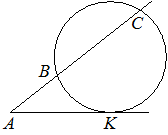 –І–µ—А–µ–Ј —В–Њ—З–Ї—Г A, –ї–µ–ґ–∞—Й—Г—О –≤–љ–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –њ—А—П–Љ—Л–µ. –Ю–і–љ–∞ –њ—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ф—А—Г–≥–∞—П –њ—А—П–Љ–∞—П –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –≤ —В–Њ—З–Ї–∞—Е B –Є C, –њ—А–Є—З—С–Љ AB=6, AC=54. –Э–∞–є–і–Є—В–µ AK.
–І–µ—А–µ–Ј —В–Њ—З–Ї—Г A, –ї–µ–ґ–∞—Й—Г—О –≤–љ–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –њ—А—П–Љ—Л–µ. –Ю–і–љ–∞ –њ—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ф—А—Г–≥–∞—П –њ—А—П–Љ–∞—П –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –≤ —В–Њ—З–Ї–∞—Е B –Є C, –њ—А–Є—З—С–Љ AB=6, AC=54. –Э–∞–є–і–Є—В–µ AK.
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –Х—Б–ї–Є —В—А–Є —Г–≥–ї–∞ –Њ–і–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л —В—А–µ–Љ —Г–≥–ї–∞–Љ –і—А—Г–≥–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–Њ —В–∞–Ї–Є–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є –њ–Њ–і–Њ–±–љ—Л.
2) –°—Г–Љ–Љ–∞ —Б–Љ–µ–ґ–љ—Л—Е —Г–≥–ї–Њ–≤ —А–∞–≤–љ–∞ 180¬∞.
3) –Ы—О–±–∞—П –Љ–µ–і–Є–∞–љ–∞ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —П–≤–ї—П–µ—В—Б—П –µ–≥–Њ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є.
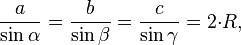 ,
,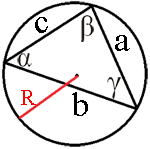
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: