
В каждой четвёртой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Аля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Аля не найдёт приз в своей банке.
Вероятность любого события равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
В данной задаче интересующее нас событие - не найти приз.
Из четырех банок 1 с призом (неблагоприятный исход), а 3 без приза (благоприятный исход). Полная группа исходов (благоприятных и неблагоприятных) = 1+3=4.
P=3/4=0,75
Ответ: P=0,75
Поделитесь решением
Присоединяйтесь к нам...
В среднем из 100 карманных фонариков, поступивших в продажу, четыре неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
На диаграмме показано распределение земель Уральского, Приволжского, Южного и Дальневосточного федеральных округов по категориям. Определите по диаграмме, в каком округе доля земель фонда запаса максимальная.

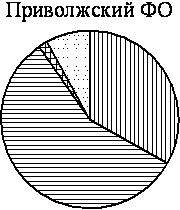


*Прочие — это земли поселений; земли промышленности и иного специального назначения; земли особо охраняемых территорий и объектов.
1) Уральский ФО
2) Приволжский ФО
3) Южный ФО
4) Дальневосточный ФО
На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему <<Параллелограмм>>, равна 0,2. Вероятность того, что это окажется задача на тему <<Площадь>> равна 0,1. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 15 с машинами и 5 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Витя. Найдите вероятность того, что Вите достанется пазл с машиной.
На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сливочных сухарях. Определите по диаграмме, в каких продуктах суммарное содержание углеводов и жиров превышает 75%.
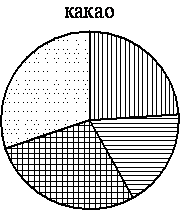
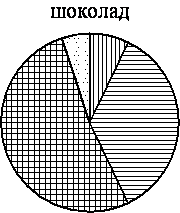



*К прочему относятся вода, витамины и минеральные вещества.
1) какао
2) шоколад
3) фасоль
4) сухари
Комментарии: