Дана арифметическая прогрессия (an), разность которой равна 0,6 и a1=6,2. Найдите сумму первых шести её членов.
Чтобы найти сумму арифметической прогрессии есть
формулы.
Воспользуемся второй формулой:
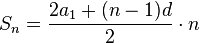
Тогда:
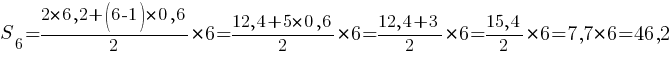
Ответ: 46,2
Поделитесь решением
Присоединяйтесь к нам...
Выписано несколько последовательных членов геометрической прогрессии: …; 1,75; x; 28; -112; … Найдите член прогрессии, обозначенный буквой x.
Выписаны первые несколько членов арифметической прогрессии: -7; -5; -3; … Найдите сумму первых пятидесяти её членов.
Дана арифметическая прогрессия: -1; 2; 5; … . Найдите сумму первых пятидесяти пяти её членов.
Записаны первые три члена арифметической прогрессии: 30; 24; 18. Какое число стоит в этой арифметической прогрессии на 51-м месте?
Записаны первые три члена арифметической прогрессии: -17; -14; -11. Какое число стоит в этой арифметической прогрессии на 81-м месте?
Хочу получать новые решения
Ни какого спама
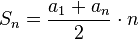, где a1 - первый член прогрессии, an - член с номером n, n — количество суммируемых членов.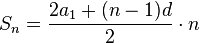, где a1 — первый член прогрессии, d — разность прогрессии, n — количество суммируемых членов. 
Автор: Таська
Комментарии: