
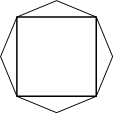
 Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
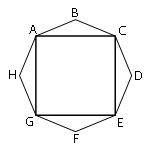 Рассмотрим треугольники ABC, CDE, EFG и GHA. AB=BC=CD=DE=EF=FG=GH=HA (по
определению правильного многоугольника).
Рассмотрим треугольники ABC, CDE, EFG и GHA. AB=BC=CD=DE=EF=FG=GH=HA (по
определению правильного многоугольника).
/ABC=/CDE=/EFG=/GHA (по
определению правильного многоугольника).
Следовательно, рассматриваемые треугольники равны (по
первому признаку равенства треугольников).
Это означает, что AC=CE=EG=GA.
Из равенства этих треугольников также следует, что все их острые углы тоже равны (/BAC=/BCA=/DCE=...и т.д.). Следовательно, /ACE=/CEG=/EGA=/GAC.
В итоге, по
определению правильного многоугольника получается, что ACEG - правильный многоугольник. А т.к. этот многоугольник имеет 4 угла, то это
квадрат.
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
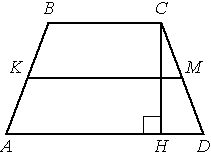 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
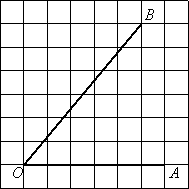 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
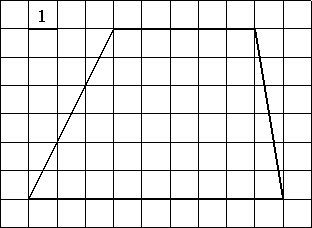 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии: