Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
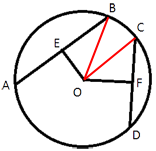Проведем отрезки OB и OC, как показано на рисунке.
Расстоянием от точки до прямой является длина перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои
хорды пополам (по
свойству хорды)
Получается, что треугольники OEB и OCF -
прямоугольные, EB=AB/2 и CF=CD/2.
По
теореме Пифагора:
OB2=OE2+EB2
OB2=242+(20/2)2
OB2=576+100=676
OB=√676=26
OB=OC=26 (т.к. OB и OC - радиусы окружности)
По
теореме Пифагора:
OC2=CF2+FO2
OC2=(CD/2)2+FO2
262=(48/2)2+FO2
676=576+FO2
FO2=676-576=100
FO=√100=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
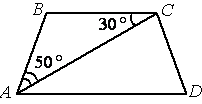Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Площадь прямоугольного треугольника равна
722√
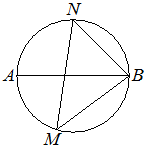На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Хочу получать новые решения
Ни какого спама
Автор: Таська
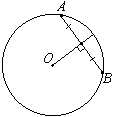
Комментарии: