ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
Вариант 1 (Предложил пользователь Светлана)
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠DOE) равен 360°/9=40°
Тогда ∠BOG, который опирается на дугу BCDEFG равен:
∠BOG=40°*5=200°
∠BOG является
центральным, следовательно градусная мера дуги BCDEFG тоже равна 200°
∠BAG тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠BAG=200°/2=100° (по
теореме о вписанном угле)
Ответ: 100
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
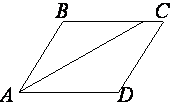Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-10-18 17:24:17) Валентина: Иногда знания отягощают,т.е.уводят от простого решения.
(2015-01-30 10:48:28) Администратор: Светлана, гениально! Обязательно добавлю Ваше решение...
(2015-01-30 10:25:17) Светлана: Такие задачи проще решать через дугу и вписанный угол. Вписанный угол равен половине дуги на которую опирается. Любой правильный многоугольник можно вписать в окружность. Вершины девятиугольника разделят окружность на 9 дуг, каждая из которых будет равна 40 градусам. Данный угол будет опираться на дугу в 200 градусов. 200:2=100.