В трапеции
ABCD AB=CD, /BDA=67° и /BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
Обратите внимание, рисунок не соответствует условию задачи (углы на рисунке заведомо меньше, чем в условии).
/ADC=/BDA+/BDC=67°+28°=95°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, /BAD=/ADC=95°.
Сумма углов любого выпуклого n-угольника равна 180°*(n-2).
Тогда сумма углов трапеции равна 180°*(4-2)=360°, следовательно /ABC+/BCD=360°-95°-95°=170°
По тому же
свойству равнобедренной трапеции /ABC=/BCD, тогда каждый из этих углов равен 170°/2=85°
В любой трапеции основания параллельны (по
определению), т.е. AD||BC, тогда, рассматривая BD как секущую, заметим, что /CBD=/BDA=67° (т.к. это
внутренние накрест лежащие углы).
Тогда /ABD=/ABC-/CBD=85°-67°=18°
Ответ: /ABD=18°
Поделитесь решением
Присоединяйтесь к нам...
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
В трапеции ABCD известно, что AD=4, BC=2, а её площадь равна 69. Найдите площадь треугольника ABC.
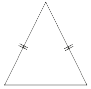Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: