
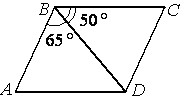 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
По
свойству
параллелограмма ∠B=∠D=65°+50°=115° и ∠A=∠C.
Найдем углы A и C.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть BD как секущую к этим параллельным прямым, то становится очевидным, что ∠CBD=∠ADB=50° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника мы можем написать: 180°=∠ABD+∠BDA+∠A
180°=65°+50°+∠A
∠A=65°=∠C
115>65, следовательно углы A и C - меньшие.
Ответ: 65
Поделитесь решением
Присоединяйтесь к нам...
 В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
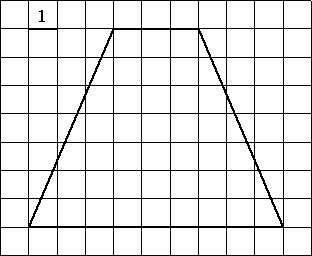 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
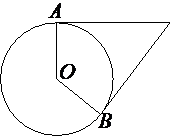 Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
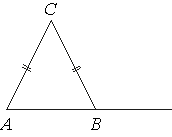 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
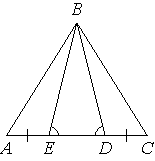 На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
Комментарии: