
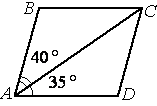 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
По
свойству
параллелограмма /A=/C=35°+40°=75° и /B=/D.
Найдем углы B и D.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть AC как секущую к этим параллельным прямым, то становится очевидным, что /DAC=/BCA=35° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABC.
По
теореме о сумме углов треугольника мы можем написать: 180°=/CAB+/B+/BCA
180°=40°+/B+35°
/B=105°=/D
105>75, следовательно углы B и D - бОльшие.
Ответ: больший угол равен 105°.
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 968√
Площадь прямоугольного треугольника равна 968√
Синус острого угла A треугольника ABC равен 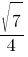 . Найдите CosA.
. Найдите CosA.
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
 Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
 Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Комментарии: