
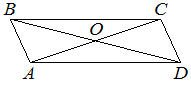
 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
По
третьему свойству параллелограмма:
DO=BD/2=20/2=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
Синус острого угла A треугольника ABC равен  . Найдите CosA.
. Найдите CosA.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
 Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
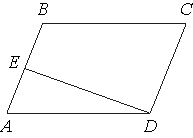 Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Комментарии:
(2023-05-16 11:36:07) : Диогонали AC и BD параллелограмма ABCD пересекаются в точке O AC=20 BD=26 AB= 8 Найдите DO