
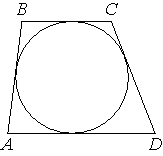 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Так как в трапецию вписана
окружность, то:
AD+BC=AВ+CD (по четвертому свойству трапеции).
AD+13=14+22
AD=14+22-13=23
Ответ: 23
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
 Катеты прямоугольного треугольника равны 3√
Катеты прямоугольного треугольника равны 3√
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
 Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Комментарии:
(2019-12-25 08:18:36) С.: трапеция абсд с основаниями ад и бс вписана в окружность. так,что ад-диаметр окружности .Диагональ трапеции равна 10 см,а её площадь - 25см2.