
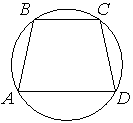
 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Так как трапеция вписана в
окружность, то ∠A+∠C=180° (по свойству описанной окружности).
∠C=180°-∠A
∠C=180°-32°=148°
Ответ: 148
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
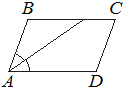 Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
 Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
 В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
Комментарии:
(2020-03-31 20:59:20) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-03-18 17:33:50) Виталик: Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 73°. Найдите угол C этой трапеции. Ответ дайте в градусах.
(2018-11-19 21:46:11) Алексей: Как бы логизчно невыозможно решить задачу со знанмиями 4 класса
(2018-11-13 22:30:17) Администратор: Алексей, эта задача не для 4-го класса. Понятие описанной окружности присутствует в условии задачи. Ее невозможно решить, основываясь на знаниях, полученных в 4-ом классе.
(2018-11-12 22:36:21) алексей: просто я в 4 классе и мы ещё не прохлдили вписанную окружность
(2018-11-12 21:36:29) Администратор: алксей, а что Вам неясно в этом решении?
(2018-11-12 14:47:29) алксей: как решать задачу?