
Какое из следующих утверждений верно?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Рассмотрим каждое утверждение:
1) "Один из двух
смежных углов острый, а другой тупой".
Острый угол - градусная мера от 0 до 90 градусов.
Прямой угол - градусная мера 90 градусов.
Тупой угол - градусная мера больше 90 градусов.
Так как сумма смежных углов равна 180°, то очевидно: если один из смежных углов больше 90°, то второй угол меньше 90°. Но если один из углов прямой (т.е. не острый и не тупой), то смежный ему угол тоже прямой. Следовательно, это утверждение неверно.
2) "Площадь
квадрата равна произведению двух его смежных сторон", это утверждение верно. Думаю, комментариев не требуется.
3) "Все хорды одной окружности равны между собой". Если рассмотреть первое свойство хорды, то становится понятно, что длина хорды зависит от ее удаленности от центра окружности, при чем диаметр - самая большая хорда. Поэтому это утверждение неверно.
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
 В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах.
 Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
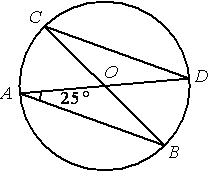 В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
 Площадь прямоугольного треугольника равна 512√
Площадь прямоугольного треугольника равна 512√
Комментарии:
(2015-12-12 17:52:00) Администратор: Галина, в утверждении не говорится, что один из углов обязательно острый. Перефразировать можно так: есть два смежных угла, утверждается, что один из них будет острый, а другой тупой. Я опровергаю это утверждение, приводя пример, когда оба угла прямые.
(2015-12-11 08:44:21) Галина: Почему в 1 утверждении, острый угол становится прямым?