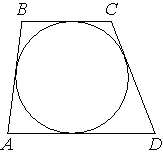Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
По
свойству вписанной в четырехугольник окружности:
AD+BC=AB+CD
AD+8=14+12
AD=14+12-8=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Найдите угол ABC. Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
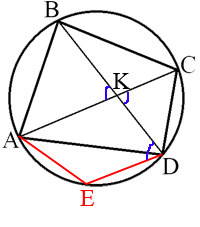Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
Хочу получать новые решения
Ни какого спама
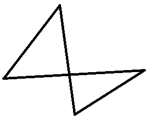(«простой»), должен быть выпуклым.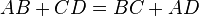
Автор: Таська
Комментарии: