Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
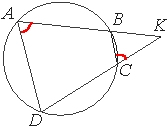По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по
свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB - является
смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.
Рассмотрим треугольникик AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
Тогда:
BK/DK=BC/AD
AD=(DK*BC)/BK=(24*18)/8=3*18=54
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
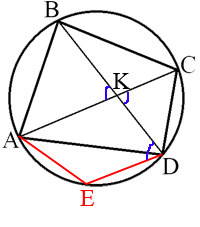Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: