
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
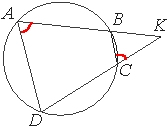 По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по
свойству описанной окружности).
По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по
свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB - является
смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.
Рассмотрим треугольникик AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
Тогда:
BK/DK=BC/AD
AD=(DK*BC)/BK=(12*6)/8=(3*6)/2=3*3=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
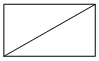 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
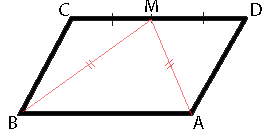 В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
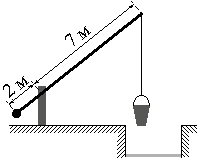 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
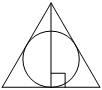 Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
 Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.

Комментарии: