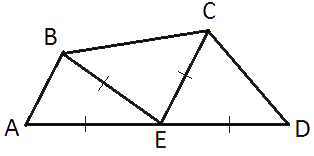
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Вариант №1
Сумма углов любого выпуклого n-угольника равна (n-2)180, тогда сумма углов четырехугольника (4-2)180=360.
Т.е. ∠A+∠B+∠C+∠D=360
∠A+92°+148°+∠D=360°
∠A+∠D=120°
Треугольники AEB, BEC и ECD -
равнобедренные, т.к. стороны AE=EB=EC=ED.
Следовательно:
∠A=∠ABE
∠EBC=∠ECB
∠ECD=∠D
Использую сумму углов четырехугольника, запишем:
∠A+∠ABE+∠EBC+∠ECB+∠ECD+∠D=360°
Используя ранее полученные равенства, запишем:
∠A+∠A+2∠EBC+∠D+∠D=360°
2∠A+2∠EBC+2∠D=360°
∠A+∠EBC+∠D=180°
120°+∠EBC=180°
∠EBC=60°
Рассмотрим треугольник EBC.
По
теореме о сумме углов треугольника ∠BEC тоже равен 60°.
Следовательно треугольник EBC -
равносторонний (по
свойству).
Значит BC=BE=EC=8 (по
определению) и
8=BE=EC=AE (по условию задачи).
AD=AE+ED=8+8=16
Ответ: AD=16
Поделитесь решением
Присоединяйтесь к нам...
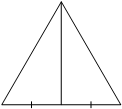Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
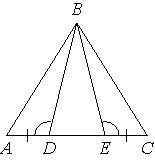На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
В трапеции ABCD основания AD и BC равны соответственно 48 и 3, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=3.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-28 21:55:05) Администратор: Alissa, хорошее решение, я решил опубликовать его от Вашего имени. Спасибо!
(2017-05-19 21:22:32) Alissa: Очевидно, что АВСD- четырёхугольник,вписанный в окружность. Значит сумма противолежащих углов А+С=В+D=180 градусам.Тогда угол D=180-92=88,угол ЕСD=88.По условию угол С=148,тогда угол ВСЕ=148-88=60.И треугольник ВСЕ равносторонний и т.д