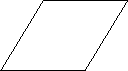
Площадь ромба равна 30, а периметр равен 24. Найдите высоту ромба.
Все стороны ромба равны (по
определению).
Поэтому P=24=4a, где а - сторона ромба.
a=24/4=6
S=ah, где h -
высота ромба.
30=S=ah=6h
h=30/6=5
Ответ: h=5
Поделитесь решением
Присоединяйтесь к нам...
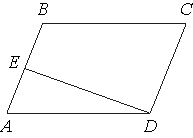Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
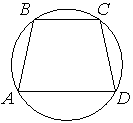Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80. Найдите расстояние от хорды AB до параллельной ей касательной k.
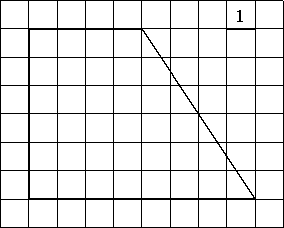Найдите площадь трапеции, изображённой на рисунке.
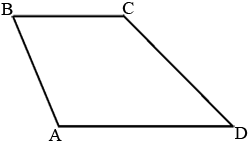Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: