Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
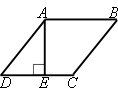150° - это тупой угол, т.е. это ∠DAB и ∠BCD (эти углы равны по
свойству параллелограмма и ромба).
AB||CD (по определению параллелограмма и ромба).
Тогда:
∠DEA=∠BAE=90° (это
накрест лежащие углы).
Следовательно:
∠DAE=∠DAB-∠EAB=150°-90°=60°
Треугольник DAE - прямоугольный, тогда, по определению косинуса:
cos∠EAB=AE/AD
cos60°=AE/38
1/2=AE/38 (по таблице косинусов)
AE=38/2=19 - это и есть
высота.
Ответ: 19
Поделитесь решением
Присоединяйтесь к нам...
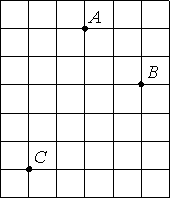На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
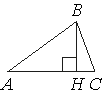В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-12-19 12:31:20) Fdggf: Fezzxc!???