В параллелограмме ABCD диагонали делят его углы пополам и равны 40 и 42. Найдите периметр параллелограмма ABCD.
Обязательно чертим рисунок по условию:
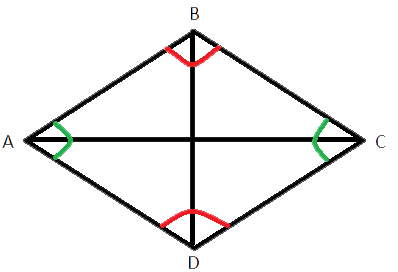
По третьему свойству ромба получается, что данный параллелограмм является ромбом.
Следовательно:
1. Все стороны равны по определению
ромба.
2. По 4-му свойству ромба:
AC2+BD2=4*a2, где a - длина стороны ромба.
Подставляем значения:
402+422=4*a2
1600+1764=4*a2
3364=4*a2
a2=3364/4=841
a=√841=29
Периметр равен сумме длин всех сторон, то есть:
P=a+a+a+a=4a=4*29=116
Ответ: 116
Поделитесь решением
Присоединяйтесь к нам...
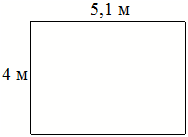На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
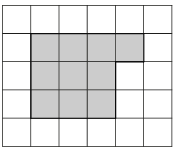План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
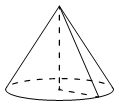Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.
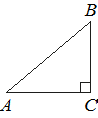В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
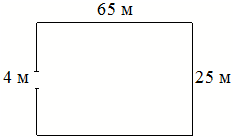Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: