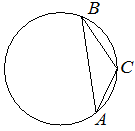
В треугольнике ABC угол C равен 120°, AB=22√3. Найдите радиус окружности, описанной около этого треугольника.
Вокруг треугольника описана окружность.
Тогда удобней всего воспользоваться
теоремой синусов:
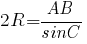
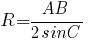
Подставляем значения:
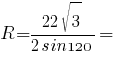
По
таблице синусов:
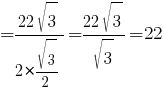
Ответ: 22
Поделитесь решением
Присоединяйтесь к нам...
Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=34.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-04-06 11:32:09) ира: задача №39Е079