
 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах.
Центр
описанной окружности располагается на пересечении
серединных перпендикуляров треугольника. Так как треугольник
равнобедренный, то
биссектриса и
серединный перпендикуляр, проведенные к основанию, совпадают.
Следовательно, BO -
биссектриса угла ABC.
Тогда: ∠CBO=∠ABC/2=177°/2=88,5°
Треугольник OBC -
равнобедренный, так как OB и OC - радиусы окружности и следовательно равны.
По
свойству равнобедренного треугольника:
∠CBO=∠BCO=88,5°
По
теореме о сумме углов треугольника:
180°=∠CBO+∠BCO+∠BOC
180°=88,5°+88,5°+∠BOC
∠BOC=3°
Ответ: 3
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 968√
Площадь прямоугольного треугольника равна 968√
 В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
 Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
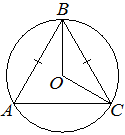 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
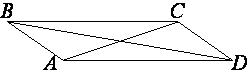 В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.



Комментарии:
(2017-03-06 23:01:34) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-03-04 19:40:30) : На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 32°. Найдите угол NMB. Ответ дайте в градусах.