Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Рассмотрим треугольник BDH.
Данный треугольник
прямоугольный, следовательно можно применить
теорему Пифагора:
BD2=HD2+BH2
532=282+BH2
2809=784+BH2
BH2=2025
BH=45
Найдем площадь
параллелограмма:
S=AD*BH=(AH+HD)*BH=(1+28)*45=1305
Ответ: 1305
Поделитесь решением
Присоединяйтесь к нам...
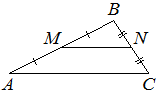Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: