
 Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Площадь
трапеции равна произведению высоты на полусумму оснований:
SABCD=h*(BC+AD)/2=h*l, где l -
средняя линия трапеции l=(BC+AD)/2. Следовательно, нам надо найти высоту h.
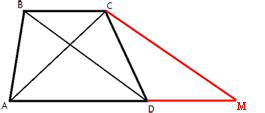 Продлим основание AD и проведем отрезок из вершины C, параллельный BD до пересечения с продленным основанием в точке M (как показано на рисунке).
Продлим основание AD и проведем отрезок из вершины C, параллельный BD до пересечения с продленным основанием в точке M (как показано на рисунке).
В четырехугольнике BCMD сторона CM||BD (мы сами так провели СМ) и DM||BC (по определению
трапеции).
Следовательно, четырехугольник BCMD -
параллелограмм.
Тогда, по
свойству параллелограмма, DM=BC.
AM=AD+DM=AD+BC=2l=2*10=20
Рассмотрим треугольник ACM.
Мы знаем длины всех его сторон, следовательно можем найти площадь через полупериметр:
Полупериметр p=(AC+CM+AM)/2=(AC+BD+AM)/2=(13+11+20)/2=22
SACM=√
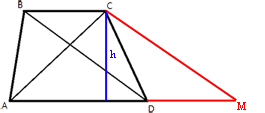 По другой формуле SACM=h*AM/2=66
По другой формуле SACM=h*AM/2=66
h=2*66/AM=2*66/20=6,6
Теперь мы можем вычислить площадь трапеции:
SABCD=h*l=6,6*10=66
Ответ: 66
Поделитесь решением
Присоединяйтесь к нам...
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
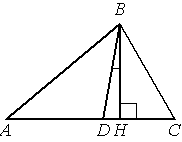 В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
 В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
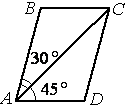 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.

Комментарии: