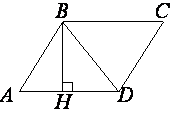Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
Площадь
параллелограмма равна произведению высоты на сторону параллелограмма. Sпараллелограмма=BH*AD
Найдем высоту. По
теореме Пифагора запишем:
BD2=HD2+BH2
852=752+BH2
7225=5625+BH2
BH2=1600
BH=40
Sпараллелограмма=BH*AD=BH*(AH+HD)=40*(6+75)=40*81=3240
Ответ: Sпараллелограмма=3240
Поделитесь решением
Присоединяйтесь к нам...
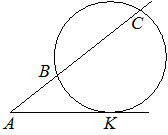Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 37°, угол ABC равен 25°. Найдите угол ACB. Ответ дайте в градусах.
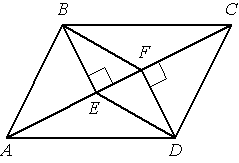В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: