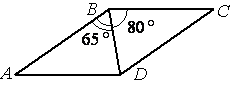Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
По
свойству
параллелограмма /B=/D=65°+80°=145° и /A=/C.
Найдем углы A и C.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть BD как секущую к этим параллельным прямым, то становится очевидным, что /CBD=/ADB=80° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника мы можем написать: 180°=/ABD+/BDA+/A
180°=65°+80°+/A
/A=35°=/C
145>35, следовательно углы A и C - меньшие.
Ответ: меньший угол равен 35°.
Поделитесь решением
Присоединяйтесь к нам...
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Найдите площадь квадрата, если его диагональ равна 1.
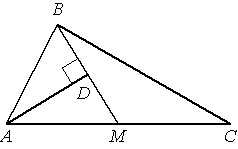Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
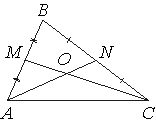Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 80°. Найдите величину угла OCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: