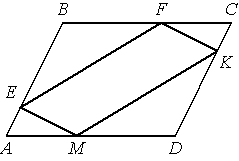
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
1) Рассмотрим треугольники АЕМ и CKF.
АЕ=CK (по условию задачи)
/A=/C (по
свойству параллелограмма)
СF=АM (по условию задачи).
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
2) Рассмотрим треугольники EBF и KDM.
Т.к. AB=CD и AD=BC (по
свойству параллелограмма), а АЕ = CK и СF = АM (по условию задачи), то BE=KD и BF=DM.
/B=/D (по
свойству параллелограмма).
Следовательно, треугольники EBF и KDM (по первому признаку). А это значит, что EF=KM.
Из пунктов 1 и 2 (равенство сторон) следует, что EFKM —
параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
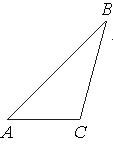В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Найдите площадь параллелограмма, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: