Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
Рассмотрим треугольник ABO.
По
определению,
ромб это
параллелограмм с равными сторонами, следовательно, на
ромб распространяются все
свойства параллелограмма.
Тогда, диагонали
ромба точкой пересечения делятся пополам (по
третьему свойству параллелограмма), т.е. OB=68/2=34
Треугольник ABO -
прямоугольный, так как ОА - расстояние до стороны
ромба, т.е. образует прямой угол со стороной.
sin∠ABO=AO/BO=17/34=1/2 => ∠ABO=30° (
табличное значение).
Треугольники EBO и CBO равны (по
трем сторонам).
Следовательно, ∠EBO=∠CBO=30°
Таким образом, ∠EBC=30°*2=60°
По свойству параллелограмма, ∠EBC=∠EDC=60° и ∠BED=∠BCD
Сумма углов любого четырехугольника равна 360°, следовательно:
∠BED=∠BCD=(360°-(2*60°))=(360°-120°)/2=120°
Ответ: 60 и 120
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=5, AC=3.
Найдите tgB.
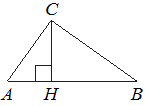На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: